Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
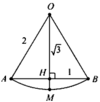
Gọi H, M lần lượt là giao điểm của d với AB và dây cung A B ⏜
Tam giác O A B đều cạnh 2 ⇒ O H = O A 3 2 = 3 ⇒ H M = 2 − 3
Quay tam giác O A B quanh trục d ta được khối nón N có bán kính đáy r = A H = 1 và chiều cao h = O H = 3
⇒ Thể tích khối nón N là V N = 1 3 π r 2 h = 3 3 π
Quay phần hình còn lại quanh trục d ta được chỏm cầu C có bán kính đáy r = A H = 1 và chiều cao h = H M = 2 − 3
⇒ Thể tích khối nón C là V C = π h 6 3 r 2 + h 2 = 16 − 9 3 3 π
Vậy thể tích khối tròn xoay (H) là
V = V N + V C = 16 − 8 3 3 π ≈ 2 , 24
Đáp án B
Giari thích các bước :
Gọi H, M lần lượt là giao điểm của d với AB và dây cung A B ⏜
Tam giác O A B đều cạnh 2 ⇒ O H = O A 3 2 = 3 ⇒ H M = 2 − 3
Quay tam giác O A B quanh trục d ta được khối nón N có bán kính đáy r = A H = 1 và chiều cao h = O H = 3
⇒ Thể tích khối nón N là V N = 1 3 π r 2 h = 3 3 π
Quay phần hình còn lại quanh trục d ta được chỏm cầu C có bán kính đáy r = A H = 1 và chiều cao h = H M = 2 − 3
⇒ Thể tích khối nón C là V C = π h 6 3 r 2 + h 2 = 16 − 9 3 3 π
Vậy thể tích khối tròn xoay (H) là
V = V N + V C = 16 − 8 3 3 π ≈ 2 , 24

Đáp án D
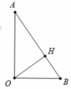
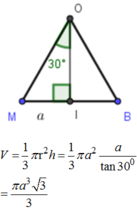
Ta có O A . sin O A H ^ = O H = a ⇒ O A = 2 a
Lại có O B = O A tan A ^ = 2 a 3 suy ra thể tích khối nón tròn xoay tạo bởi tam giác AOB khi quay quanh trục OA là V = 1 3 πOB 2 . OA = 8 9 πa 3

Đáp án C
Thể tích khối nón là: V = 1 3 π . A C 2 . A B = 1 3 π .4 2 .3 = 16 π c m 3 .

Đáp án A
Khi quay ∆ O A B quanh trục Oy, ta được hình nón có bán kính đáy r = OA và chiều cao h = OB. Theo bài ra, ta có OA + OB = r + h = 1 với (0 < r, h < 1)
Khi đó, thể tích khối nón là V N = 1 3 πr 2 h = 1 3 πr 2 1 - r .
Ta có r 2 1 - r 2 = 4 . r 2 . r 2 . 1 - r ≤ 4 . r 2 + r 2 + 1 - r 3 27 = 4 27 ⇒ V N ≤ 1 3 π . 4 27 = 4 π 81 .
Tham khảo: Ta có thể đưa điểm B có tung độ âm về tung độ dương thì thể tích của khối nón không đổi.
Gọi A a ; 0 B 0 ; b a , b > 0 suy ra phương trình đường thẳng A B : x y + y b = 1 ⇒ x = a - a b . y .
Khi đó V O y = π . ∫ a b a - a b y 2 d y = πa 2 b 3 .
Ta có 4 π 3 . a 2 . a 2 . b ≤ 4 π 3 . a 2 + a 2 + b 3 27 = 4 π 81 ⇒ V M a x = 4 π 81 .

Đáp án B.
Đặt a = B C , b = C A , c = A B .
Quay tam giác OCA quanh trung trực của đoạn thẳng CA thì khối tròn xoay sinh ra là khối nón có chiều cao h 1 = R 2 − 1 4 b 2 và bán kính đáy r 1 = 1 2 b nên ta có V 1 = 1 3 π r 1 2 h 1 = 1 24 π b 2 4 R 2 − b 2 .
Tương tự, ta có
V 2 = 1 24 π c 2 4 R 2 − c 2 ; V 3 = 1 24 π a 2 4 R 2 − a 2 .
Bằng việc khảo sát hàm số f t = t 2 4 R 2 − t trên khoảng 0 ; 4 R 2 hoặc dựa vào bất đẳng thức Cô-si
1 2 b 2 . 1 2 b 2 . 4 R 2 − b 2 ≤ 1 2 b 2 + 1 2 b 2 + 4 R 2 − b 2 3 3 = 64 27 R 6 .
Ta được V 1 ≤ 2 π 3 9 R 3 ; V 2 ≤ 2 π 3 9 R 3 . Suy ra V 1 + V 2 ≤ 4 π 3 9 R 3 .
Dấu bằng xảy ra khi và chỉ khi b = c = 2 6 3 R .
Vậy V 1 + V 2 đạt giá trị lớn nhất bằng 4 π 3 9 R 3 khi b = c = 2 6 3 R .
Khi đó tam giác ABC cân tại A và có A B = A C = 2 6 3 R .
Gọi AH là đường cao của tam giác ABC thì 2 R . A H = A B 2 . Từ đó suy ra A H = A B 2 2 R = 4 3 R . Do đó O H = A H − R = 1 3 R và a = 2 R 2 − O H 2 = 4 2 3 R .
Suy ra V 3 = 8 π 81 R 3 .

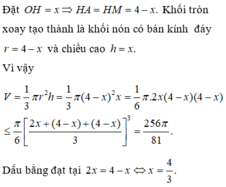
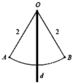

Chọn đáp án D