Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét (O) có
^BMC = ^BNC = 900 ( góc nt chắn nửa đường tròn )
=> ^AMD = ^AND = 900
Xét tứ giác AMDN có
^AMD + ^AND = 1800
mà 2 góc này đối
Vậy tứ giác AMDN nt 1 đương tròn
b, Ta có ^MAD = ^MND ( góc nt chắn cung MD của tứ giác AMDN )
mà ^MNB = ^MCB ( góc nt chắn cung MB )
Xét tứ giác OMC có OM = OC = R
Vậy tam giác OMC cân tại O
=> ^OMC = ^OCM
=> ^OMC = ^MAD

a: BE,BD là hai tia phân giác của hai góc kề bù
=>BE vuông góc BD
CE,CD là hai tia phân giác của hai góc kề bù
=>CE vuông góc CD
Xét tứ giác EBDC có
góc EBD+góc ECD=180 độ
=>EBDC nội tiếp
b: Xét ΔIBE và ΔIDCcó
góc IBE=góc IDC
góc BIE=góc DIC
=>ΔIBE đồng dạng với ΔIDC
=>IB/ID=IE/IC
=>IB*IC=ID*IE

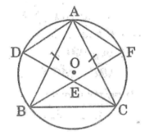
Theo giả thuyết suy ra các cung bằng nhau :
\(\widebat{AD}=\widebat{AF}=\widebat{DB}=\widebat{FC}\)
Do đó \(\widehat{A_1}=\widehat{B_1}\)mà 2 góc ở vị trí sole trong \(\Rightarrow AD//EF\) \(\left(1\right)\)
\(\widehat{A_2}=\widehat{C}_1\) mà 2 góc ở vị trí sole trong \(\Rightarrow AF//CD\) \(\left(2\right)\)
và \(AD=EF\) \(\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\Rightarrow\)ADEF là hình thoi


a: góc ANE=1/2(sđ cung AE+sđ cung CD)
=1/2(sđ cung AE+sđ cung BD)
góc AIE=1/2(sđ cung AE+sđ cung BD)
=>góc ANE=góc AIE
=>AINE nội tiếp
góc BMD=1/2(sđ cung BD+sđ cung CE)
góc BID=1/2(sđ cung BD+sđ cung AE)
mà sđ cung CE=sđ cung AE
nên góc BMD=góc BID
=>BIMD nội tiếp