K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

5 tháng 1 2022
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
Xét tứ giác BDNC có
DN//BC
BD//NC
Do đó: BDNC là hình bình hành
b: Xét tứ giác BDNH có BH//DN
nên BDNH là hình thang

5 tháng 3 2022
Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
hay BMNC là hình thang
b: Xét ΔABK có MI//BK
nên MI/BK=AM/AB=1/2(1)
XétΔACK có NI//CK
nên NI/CK=AN/AC=1/2(2)
Từ (1)và (2) suy ra MI/BK=NI/CK
mà MI=NI
nên BK=CK
hay K là trug điểm của BC
Xét ΔABC có
K là trung điểm của BC
M là trung điểm của AB
Do đó: KM là đường trung bình
=>KM//AN và KM=AN
hay AMKN là hình bình hành
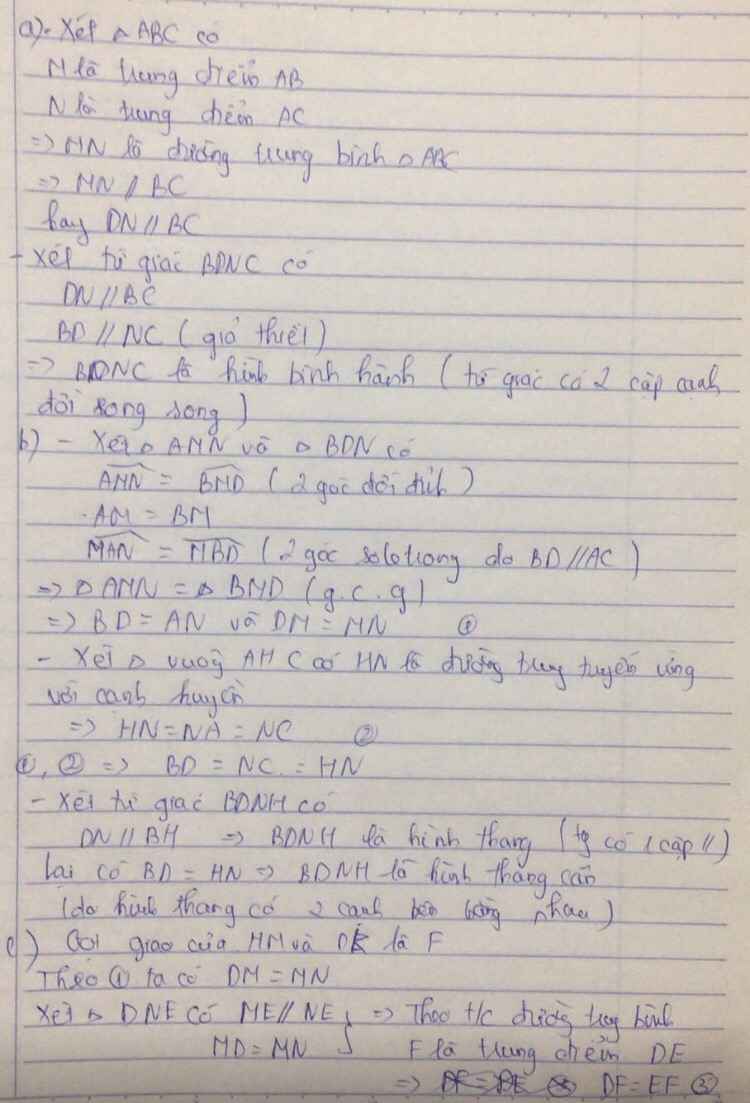

Hướng dẫn a,b
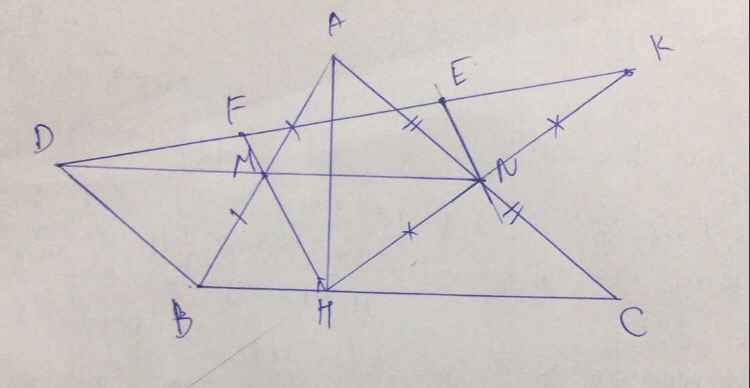
Tự vẽ hình
a) M , N là trung điểm AB , AC => MN là đường trung bình của tam giác ABC
=> MN//BC => DN//BC . Mà BD// NC => Tứ giác BDNC là hbh
b) Có \(\widehat{NCH}=\widehat{NDB}\) ( hình bình hành )
Tam giác AHC vuông có trung tuyến HN = 1/2 AC = NC => Tam giác NHC cân => \(\widehat{NCH}=\widehat{NHC}\)
=> \(\widehat{NDB}=\widehat{NHC}\)
Mà NHC = NHD (so le trong ) = > NHD = NBD
=> BDNH là hình thang cân