Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo lời giải tại đây:
https://hoc24.vn/hoi-dap/tim-kiem?id=62067&q=cho%20tam%20gi%C3%A1c%20ABC%20nh%E1%BB%8Dn%20c%C3%B3%20BC%3Da%3B%20AC%3Db%3B%20AB%3Dc%3BCMR%3A%20a%2FsinA%3Db%2FsinB%3Dc%2Fsin%20C

Từ A vẽ AD _|_ BC ,AG là trung tuyến cắt BC tại E\(\Rightarrow\)\(\hept{\begin{cases}AD\le AE\Rightarrow\frac{1}{AD}\ge\frac{1}{AE}\\1.2GE=BC\left(do\Delta BGCvuongcoElatrungdiem\right)\end{cases}}\)
cotB=\(\frac{BD}{AD}\)cotC=\(\frac{CD}{AD}\)\(\Rightarrow\)2.cotB + cotC=\(\frac{BC}{AD}\)
3.G là trực tâm nên 3GE=AE\(\Rightarrow\)\(\frac{1}{AD}\ge\frac{1}{3GE}\)
từ 1, 2 và 3 \(\Rightarrow\)cotB + cotC=\(\frac{BC}{AD}\ge\frac{2GE}{3GE}=\frac{2}{3}\)

Trong trường hợp góc A vuông thì bài toán trở thành: \(a^2=b^2+c^2\) đúng theo Pitago
Trong trường hợp góc A nhọn:
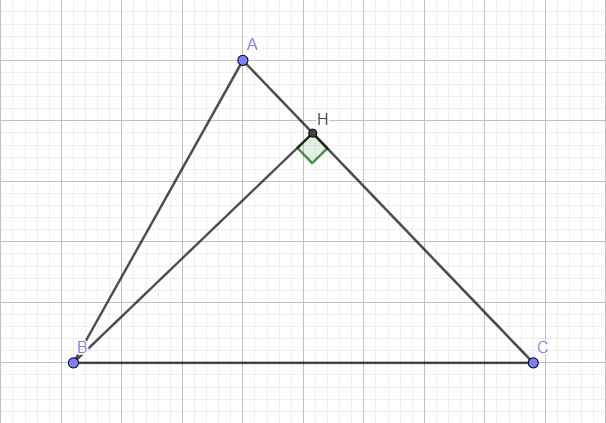
Kẻ đường cao BH (H thuộc AC) \(\Rightarrow AH=AB.cosA=c.cosA\)
Áp dụng định lý Pitago cho tam giác vuông ABH:
\(BH^2=AB^2-AH^2=c^2-AH^2\)
Áp dụng định lý Pitago cho tam giác vuông BCH:
\(BC^2=BH^2+CH^2\Leftrightarrow a^2=c^2-AH^2+CH^2\)
\(\Leftrightarrow a^2=c^2-AH^2+\left(AC-AH\right)^2=c^2-AH^2+\left(AC^2-2AC.AH+AH^2\right)\)
\(\Leftrightarrow a^2=c^2-AH^2+b^2-2b.AH+AH^2\)
\(\Leftrightarrow a^2=b^2+c^2-2b.AH=b^2+c^2-2bc.cosA\) (đpcm)
Trong trường hợp góc A tù làm hoàn toàn tương tự:
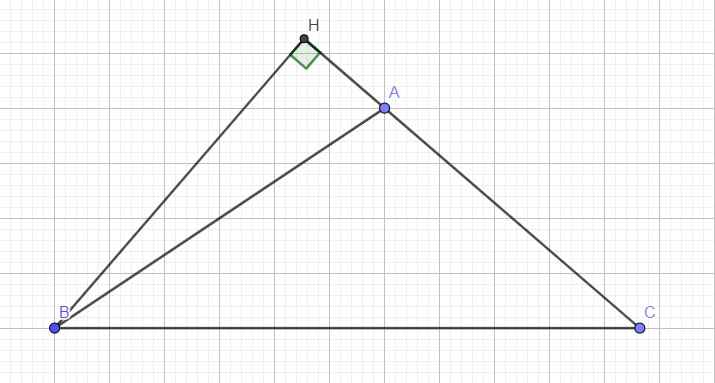
\(a^2=BH^2+CH^2=c^2-AH^2+\left(b+AH\right)^2=c^2+b^2+2b.AH\)
\(=b^2+c^2+2b.AB.cos\widehat{BAH}=b^2+c^2-2bc.cosA\)

Tự vẽ hình
Kẻ BH \(\perp\)AC và \(CK\perp\)AB
Tam giác AKC vuông tại K
=>CK=bsinA (1)
Tam giác BKC vuông tại K
=>CK=asinB (2)
Từ (1) (2)=>bsinA=asinB
<=>\(\frac{a}{sinA}=\frac{b}{sinB}\)
Chứng minh tương tự ta có :\(\frac{a}{sinA}=\frac{c}{sinC}\)
Vậy ....
