Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔMIN vuông tại I có IE là đường cao ứng với cạnh huyền MN
nên \(ME\cdot MN=MI^2\left(1\right)\)
Xét ΔMIP vuông tại I có IF là đường cao ứng với cạnh huyền MP
nên \(MF\cdot MP=MI^2\left(2\right)\)
Từ (1) và (2) suy ra \(ME\cdot MN=MF\cdot MP\)
hay \(\dfrac{ME}{MP}=\dfrac{MF}{MN}\)
Xét ΔMEF vuông tại M và ΔMPN vuông tại M có
\(\dfrac{ME}{MP}=\dfrac{MF}{MN}\)
Do đó: ΔMEF\(\sim\)ΔMPN

a: Xét ΔMIN vuông tại I có IE là đường cao ứng với cạnh huyền MN
nên \(ME\cdot MN=MI^2\left(1\right)\)
Xét ΔMIP vuông tại I có IF là đường cao ứng với cạnh huyền MP
nên \(MF\cdot MP=MI^2\left(2\right)\)
Từ (1) và (2) suy ra \(ME\cdot MN=MF\cdot MP\)
hay \(\dfrac{ME}{MP}=\dfrac{MF}{MN}\)
Xét ΔMEF vuông tại M và ΔMPN vuông tại M có
\(\dfrac{ME}{MP}=\dfrac{MF}{MN}\)
Do đó: ΔMEF\(\sim\)ΔMPN

a: Xét ΔMNP vuông tại M có
\(NP^2=MN^2+MP^2\)
hay NP=5(cm)
Xét ΔMNP vuông tại M có
\(\sin\widehat{P}=\dfrac{3}{5}\)
\(\Leftrightarrow\widehat{P}\simeq37^0\)
\(\Leftrightarrow\widehat{N}=53^0\)

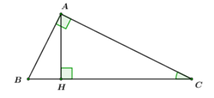
Áp dụng định lý Pytago trong ∆ ABC vuông tại A ta có:
![]()
Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
![]()
![]()
Đáp án cần chọn là: B

BÀI 1:
a)
· Trong ∆ ABC, có: AB2= BC.BH
Hay BC= ![]() =
= ![]()
· Xét ∆ ABC vuông tại A, có:
AB2= BH2+AH2
↔AH2= AB2 – BH2
↔AH= ![]() =4 (cm)
=4 (cm)
b)
· Ta có: HC=BC-BH
àHC= 8.3 - 3= 5.3 (cm)
· Trong ∆ AHC, có:

· ![]()
Bài 1:
a) Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BC=\frac{AB^2}{BH}\)
\(\Rightarrow\)\(BC=\frac{5^2}{3}=\frac{25}{3}\)
Áp dụng Pytago ta có:
\(AH^2+BH^2=AB^2\)
\(\Rightarrow\)\(AH^2=AB^2-BH^2\)
\(\Rightarrow\)\(AH^2=5^2-3^2=16\)
\(\Rightarrow\)\(AH=4\)
b) \(HC=BC-BH=\frac{25}{3}-3=\frac{16}{3}\)
Áp dụng hệ thức lượng ta có:
\(\frac{1}{HE^2}=\frac{1}{AH^2}+\frac{1}{HC^2}\)
\(\Leftrightarrow\)\(\frac{1}{HE^2}=\frac{1}{4^2}+\frac{1}{\left(\frac{16}{3}\right)^2}=\frac{25}{256}\)
\(\Rightarrow\)\(\frac{1}{HE}=\frac{5}{16}\)
\(\Rightarrow\)\(HE=\frac{16}{5}\)
\(NP=NI+PI=8\left(cm\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}MP^2=PI\cdot PN=40\\MN^2=NI\cdot PN=24\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}MP=2\sqrt{10}\left(cm\right)\\NM=2\sqrt{6}\left(cm\right)\end{matrix}\right.\)
\(P_{MPN}=MN+NP+PM=2\sqrt{10}+2\sqrt{6}+8=2\left(\sqrt{10}+\sqrt{6}+4\right)\left(cm\right)\)
Xét ΔMPN vuông tại M có MI là đường cao ứng với cạnh huyền NP, ta được:
\(\left\{{}\begin{matrix}MP^2=PI\cdot PN\\MN^2=NI\cdot NP\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}MP=2\sqrt{10}\left(cm\right)\\MN=2\sqrt{6}\left(cm\right)\end{matrix}\right.\)
\(C_{MPN}=2\sqrt{10}+2\sqrt{6}+8\left(cm\right)\)