Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác MNKP có
E là trung điểm của NP
E là trung điểm của MK
Do đó: MNKP là hình bình hành
mà \(\widehat{PMN}=90^0\)
nên MNKP là hình chữ nhật

a: Xét tứ giác MPNI có
Q là trung điểm chung của MN và PI
Do đó: MPNI là hình bình hành
b: Xét ΔNMP có NQ/NM=NK/NP
nên QK//MP
=>QK vuông góc với MN

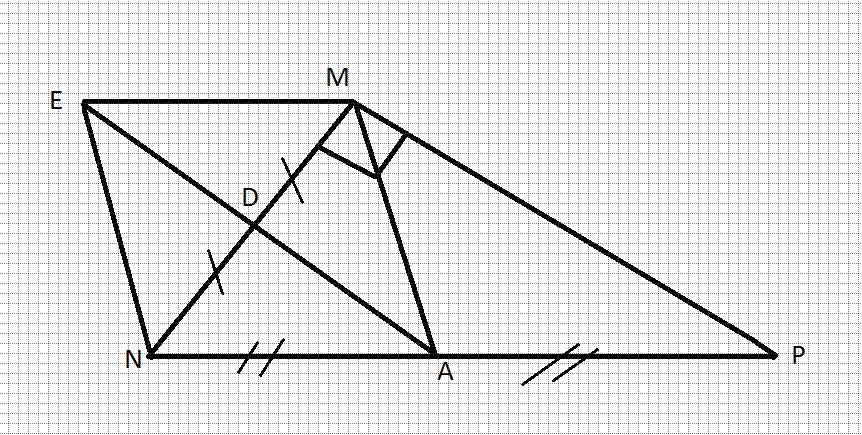
a: Xét ΔMNP có NA/NP=ND/NM
nên DA//MP
=>DA vuông góc với NM
=>EA vuông góc với NM
mà EA cắt NM tại trung điểm của EA
nên E đối xứng A qua MN
b: Xét tứ giác MENA có
D là trung điểm chung của MN và EA
AN=AM
Do đó: MENA là hình thoi

b: Xét tứ giác AMHI có
AM//HI
HM//AI
Do đó: AMHI là hình bình hành
mà \(\widehat{MAI}=90^0\)
nên AMHI là hình chữ nhật
Suy ra: AH=MI

a: Xét tứ giác AHDE có
I là trung điểm của AD
I là trung điểm của HE
Do đó: AHDE là hình bình hành
mà AD⊥HE
nên AHDE là hình thoi

a: Ta có: Q và A đối xứng với nhau qua MN
nên MN là đường trung trực của QA
=>MN vuông góc với QA tại trung điểm của QA
Ta có: Q và B đối xứng với nhau qua MP
nên MP là đường trung trực của QB
=>MP vuông góc với QB tại trung điểm của QB
Xét tứ giác MRQS có
\(\widehat{MRQ}=\widehat{MSQ}=\widehat{SMR}=90^0\)
Do đó: MRQS là hình chữ nhật
b: Xét ΔMNP có
Q là trung điểm của NP
QS//MN
Do đó: S là trung điểm của MP
Xét tứ giác MQPB có
S là trung điểm của MP
S là trung điểm của QB
Do đó: MQPB là hình bình hành
mà QM=QP
nên MQPB là hình thoi