Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔMNI và ΔMPI có
MN=MP
NI=PI
MI chung
Do đó: ΔMNI=ΔMPI
b: Ta có: ΔMNP cân tại M
mà MI là đường trung tuyến
nên MI là đường trung tuyến
c: Ta có: ΔMNP cân tại M
mà MI là đường trung tuyến
nên MI là đường cao

a: Xét ΔMNI vuông tại M và ΔKNI vuông tại K có
NI chung
\(\widehat{MNI}=\widehat{KNI}\)
Do đó: ΔMNI=ΔKNI
b: Ta có: ΔMNI=ΔKNI
nên NM=NK
Xét ΔNMK có NM=NK
nên ΔNMK cân tại N
mà \(\widehat{MNK}=60^0\)
nên ΔNMK đều
c: Ta có: ΔMNI=ΔKNI
nên MI=IK
mà IK<IP
nên MI<IP
d: Xét ΔMNP vuông tại M có
\(NP=\dfrac{MN}{\sin30^0}\)
\(=3:\dfrac{1}{2}=6\left(cm\right)\)
Áp dụng định lí Pytago vào ΔMNP vuông tại M, ta được:
\(MN^2+MP^2=NP^2\)
\(\Leftrightarrow MP=3\sqrt{3}\left(cm\right)\)

a: Xét ΔMNI vuông tại M và ΔKNI vuông tại K có
NI chung
\(\widehat{MNI}=\widehat{KNI}\)
Do đó: ΔMNI=ΔKNI
b: Ta có: ΔMNI=ΔKNI
nên NM=NK
Xét ΔMNK có NM=NK
nên ΔMNK cân tại N
Xét ΔMNK cân tại N có \(\widehat{MNK}=60^0\)
nên ΔMNK đều
c: Ta có: ΔMNI=ΔKNI
nên MI=IK
mà IK<IP
nên MI<IP
d: Xét ΔMNP vuông tại M có
\(NP=\dfrac{MN}{\sin30^0}\)
\(=3:\dfrac{1}{2}=6\left(cm\right)\)
Áp dụng định lí Pytago vào ΔMNP vuông tại M, ta được:
\(MN^2+MP^2=NP^2\)
\(\Leftrightarrow MP=3\sqrt{3}\left(cm\right)\)

a: ΔMNI vuông tại M
=>MN<NI và góc MIN<90 độ
=>góc NIP>90 độ
=>NI<NP
=>MN<NI<NP
b: Xét ΔIPK và ΔIMN có
IP=IM
góc PIK=góc MIN
IK=IN
=>ΔIPK=ΔIMN
c: ΔIPK=ΔIMN
=>PK=MN và goc MNI=góc PKI
d: góc MPN=90-35=55 độ

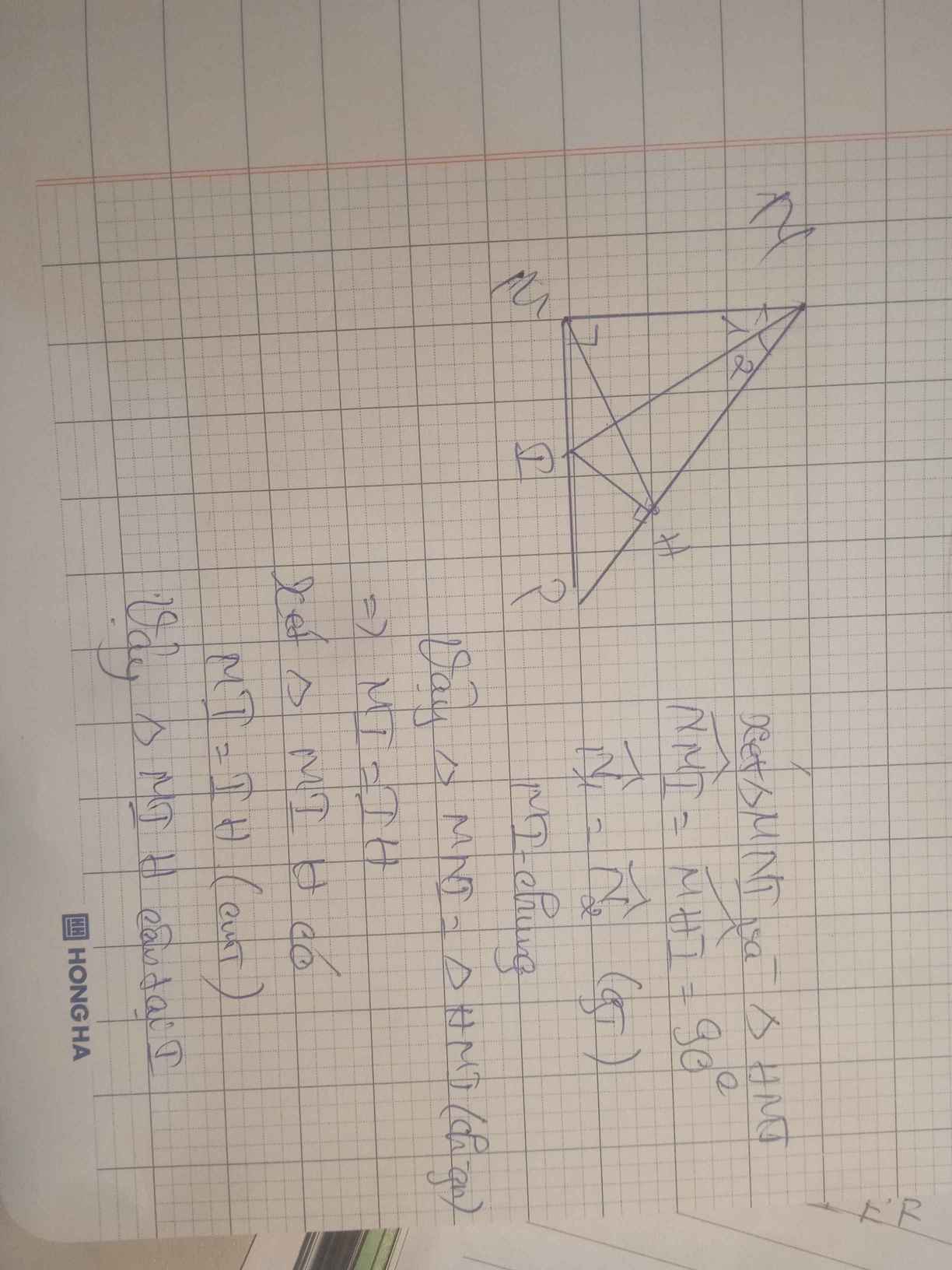
a) Xét tam giác MNI và tam giác HNI lần lượt vuông tại M và H có:
\(\widehat{MNI}=\widehat{HNI}\)( do NI là tia phân giác \(\widehat{MNI}\))
NI chung
=> ΔMNI=ΔHNI(ch-gn)
b) Ta có: ΔMNI=ΔHNI(cmt)
=> MI=IH( 2 cạnh tương ứng)
Xét tam giác HIP vuông tại H có:
IP là cạnh huyền
=> PI>IH
Mà MI=IH(cmt)
=> PI>MI
a: Xét ΔMNI vuông tại M và ΔHNI vuông tại H có
NI chung
\(\widehat{MNI}=\widehat{HNI}\)
Do đó: ΔMNI=ΔHNI
b: Ta có: ΔMNI=ΔHNI
Suy ra: MI=HI
mà HI<IP
nên PI>MI