Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ABEC có
M là trung điểm của đường chéo BC
M là trung điểm của đường chéo AE
Do đó: ABEC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABEC là hình chữ nhật

a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trung điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật

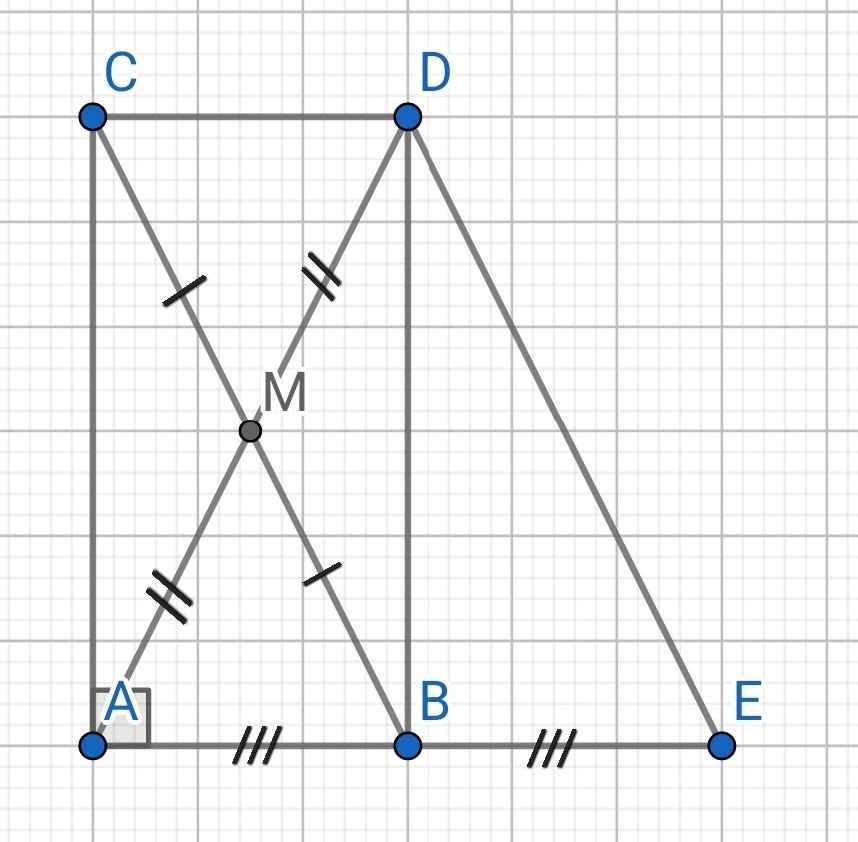 a) Tứ giác ABDC có:
a) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ABDC là hình chữ nhật
b) Do ABDC là hình chữ nhật (cmt)
⇒ CD = AB (1)
Do B là trung điểm của AE (gt)
⇒ BE = AB = AE : 2 (2)
Từ (1) và (2) ⇒ CD = BE
Do ABDC là hình chữ nhật (cmt)
⇒ CD // AB
⇒ CD // BE
Tứ giác BEDC có:
CD // BE (cmt)
CD = BE (cmt)
⇒ BEDC là hình bình hành
c) Do ABDC là hình chữ nhật (cmt)
⇒ AC // BD
Do đó AC, BD, EK đồng quy là vô lý
Em xem lại đề nhé!

a: Xét tứ giác ABNC có
O là trung điểm của BC
O là trung điểm của AN
Do đó: ABNC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABNC là hình chữ nhật



a)Xét △ABI và △CBK:
AB=BC(gt)
BI=BK(gt)
\(\widehat{ABI}=\widehat{CBK}\) (đối đỉnh)
=> △ABI=△CBK (c.g.c)
=> \(\widehat{AIB}=\widehat{CKB}\)
Mà 2 góc này ở vị trí so le trong nên AI//CK
Cmtt: \(\widehat{KAB}=\widehat{ICB}\)
Mà 2 góc này ở vị trí so le trong nên AK//CI
=> AKCI là hình bình hành
Lại có góc KAI=90 độ
=> AKCI là hình chữ nhật
b) Và AKCI là hình chữ nhật nên AK//CI và AK=CI
Lại có AK=AD
Suy ra AD//CI và AD=CI
=> ADIC là hình bình hành
KI: cạnh chung
góc