Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


⇒ AD là đường kính của đường tròn ngoại tiếp tam giác ABD Mà ABDC là tứ giác nội tiếp
⇒ AD là đường kính của đường tròn ngoại tiếp tứ giác ABDC.
⇒ tâm O là trung điểm AD.
Vậy tâm đường tròn đi qua bốn điểm A, B, D, C là trung điểm AD.
Kiến thức áp dụng
+ Một tứ giác có tổng số đo hai góc đối nhau bằng 180º thì tứ giác đó nội tiếp được đường tròn.
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.

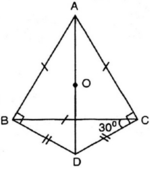
a) Theo giả thiết, =
=
.60o = 30o
=
+
(tia CB nằm giữa hai tia CA, CD)
=> = 60o + 30o = 90o (1)
Do DB = CD nên ∆BDC cân => =
= 30o
Từ đó = 60o + 30o = 90o (2)
Từ (1) và (2) có +
= 180o nên tứ giác ABDC nội tiếp được.
b) Vì = 90o nên AD là đường kính của đường tròn ngoại tiếp tứ giác ABDC, do đó tâm đường tròn ngoại tiếp tứ giác ABDC là trung điểm AD.

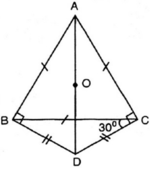
Do tam giác ABC là tam giác nên A C B ^ = 60 o
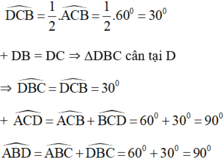
=> Tứ giác ABDC có: ![]()
=> ABDC là tứ giác nội tiếp

a)Nối F với D : E với D ta có:
Xét tam giác FBC ta có
D là trung điểm BC(1)
Góc BFC=90 (2)
Từ (1)(2)=>FD là trung tuyến của tam giác FBC
=>BD=CD=DF(*)
Chứng minh tương tự tam giác EBC
=>DE=DC=DB(**)
Từ (*)(**)=>BD=CD=DF=DE=(1/2BC)
=>B;F;E;C thuộc đừng tròn
=>D là tâm của đường tròn
B) Do B;H;E nằm trên cùng 1 đừng thẳng => H ko thuộc đừng tròn
=>B;H;E;c ko thuộc đừng tròn
Ta có: A B D ^ = 90 o
⇒ AD là đường kính của đường tròn ngoại tiếp tam giác ABD Mà ABDC là tứ giác nội tiếp
⇒ AD là đường kính của đường tròn ngoại tiếp tứ giác ABDC.
⇒ tâm O là trung điểm AD.
Vậy tâm đường tròn đi qua bốn điểm A, B, D, C là trung điểm AD.