NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
cho tam giác ABC có G là trọng tâm. Diện tích của các tam giác AGB, BGC, AGC có bằng nhau hay không?
0
LC
31 tháng 3 2017
────(♥)(♥)(♥)────(♥)(♥)(♥) __ ɪƒ ƴσυ’ʀє αʟσηє,
──(♥)██████(♥)(♥)██████(♥) ɪ’ʟʟ ɓє ƴσυʀ ѕɧα∂σѡ.
─(♥)████████(♥)████████(♥) ɪƒ ƴσυ ѡαηт тσ cʀƴ,
─(♥)██████████████████(♥) ɪ’ʟʟ ɓє ƴσυʀ ѕɧσυʟ∂єʀ.
──(♥)████████████████(♥) ɪƒ ƴσυ ѡαηт α ɧυɢ,
────(♥)████████████(♥) __ ɪ’ʟʟ ɓє ƴσυʀ ρɪʟʟσѡ.
──────(♥)████████(♥) ɪƒ ƴσυ ηєє∂ тσ ɓє ɧαρρƴ,
────────(♥)████(♥) __ ɪ’ʟʟ ɓє ƴσυʀ ѕɱɪʟє.
─────────(♥)██(♥) ɓυт αηƴтɪɱє ƴσυ ηєє∂ α ƒʀɪєη∂,
───────────(♥) __ ɪ’ʟʟ ʝυѕт ɓє ɱє.
(⁀‵⁀) ✫ ✫ ✫.
`⋎´✫¸.•°*”˜˜”*°•✫
..✫¸.•°*”˜˜”*°•.✫
☻/ღ˚ •。* ♥ ˚ ˚✰˚ ˛★* 。 ღ˛° 。* °♥ ˚ • ★ *˚ .ღ 。
/▌*˛˚ღ •˚ Type your status message ˚ ✰* ★
GOOD ♥
(¯`♥´¯).NİGHT.♥
.`•.¸.•´(¯`♥´¯)..SWEET ♥
*****.`•.¸.•´(¯`♥´¯)..DREAMS ♥
***********.`•.¸.•´(¯`♥´¯)..♥
...***************.`•.¸.•´……♥ ♥
..... (¯`v´¯)♥
.......•.¸.•´
....¸.•´
... (
☻/
/▌♥♥
/ \ ♥Type your status message♥
hello
NH
22 tháng 3 2023
tỉ số giữa AG và AD
\(\dfrac{AG}{AD}=\dfrac{2}{3}\)
bạn tự vẽ hình bài này nhé
22 tháng 3 2023
Có `G` là trọng tâm `Delta ABC`
`=>AG=2/3 AD(t/c)`
hay `(AG)/(AD)=2/3`
17 tháng 9 2023
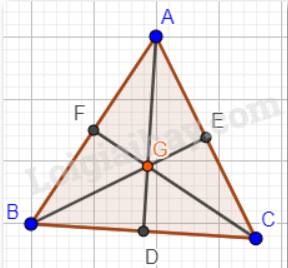
Tam giác ABC đều nên AB = AC = BC.
G là trọng tâm tam giác ABC nên AD, BE, CF là các đường trung tuyến trong tam giác.
Suy ra: AF = BF = AE = CE = BD = CD.
Xét tam giác ADB và tam giác ADC có:
AB = AC (tam giác ABC đều);
AD chung
BD = CD (D là trung điểm của đoạn thẳng BC).
Vậy \(\Delta ADB = \Delta ADC\)(c.c.c) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).
Mà ba điểm B, D, C thẳng hàng nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \)hay \(AD \bot BC\). (1)
Tương tự ta có:
\(\widehat {AEB} = \widehat {CEB} = 90^\circ \) hay\(BE \bot AC\). (2)
\(\widehat {AFC} = \widehat {BFC} = 90^\circ \) hay\(CF \bot AB\). (3)
Từ (1), (2), (3) suy ra G là giao điểm của ba đường cao AD, BE, CF.
Vậy G cũng là trực tâm của tam giác ABC.
CM
12 tháng 8 2019
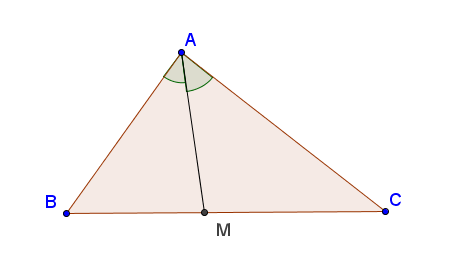
Vì tam giác ABC đều nên (BAC) ̂=60^0.
AI là tia phân giác của góc BAC nên (BAI) ̂=30^0. Chọn A
S
16 tháng 8 2016
Câu 1: (bạn tự vẽ hình nhé)
a) Xét \(\Delta\)BAH và \(\Delta\)CAH :
AHB^ = AHC^ = 90o
AB = AC
ABH^ = ACH^
=> \(\Delta\)BAH = \(\Delta\)CAH (cạnh huyền _ góc nhọn) (2)
=> BH = CH (2 cạnh tương ứng) (1)
Mà BH + CH = BC
<=> 2 * BH = 6
BH = 3 (cm)
ABH^ = ACH^
Áp dụng định lý Py-ta-go vào \(\Delta\)ABH:
BH^2 + AH^2 = AB^2
AH^2 = AB^2 - BH^2 = 5^2 - 3^2 = 25 - 9 = 16 (cm)
\(\Rightarrow AH=\sqrt{16}=4\left(cm\right)\)
b) Từ (1) => AH là đường trung tuyến của \(\Delta\)BAC
=> A, G, H thẳng hàng.
c) Từ (2) => BAH^ = CAH^ hay BAG^ = CAG^
Xét \(\Delta\)BAG và \(\Delta\)CAG:
AB = AC
BAG^ = CAG^
AG chung
=> \(\Delta\)BAG = \(\Delta\)CAG (c.g.c)
=> ABG^ = ACG^ (2 góc tương ứng)
Do tam giác ABC đều và G là trọng tâm nên \(\widehat{AGB}=\widehat{BGC}=\widehat{CGA}\)
Mà \(\widehat{AGB}+\widehat{BGC}+\widehat{CGA}=360^0\)
\(\Rightarrow3\widehat{BGC}=360^0\)
\(\Rightarrow\widehat{BGC}=120^0\)