Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có Δ A'B'C' ∈ Δ ABC theo tỉ số k
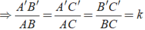
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
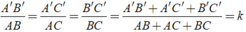
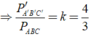
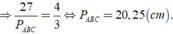

Vì tam giác ABC đồng dạng với tam giác MNP theo tỉ số 2 3 nên
A B M N = A C M P = B C N P = A B + A C + B C M N + M P + N P = P A B C P M N P
và A B M N = 2 3 ⇒ P A B C P M N P = 2 3
Từ đó P M N P = 3 P A B C 2 = 3.40 2 = 60 c m
Đáp án: A

ΔABC~ΔDEF theo hệ số tỉ lệ là k=2/3
=>\(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{2}{3}\)
=>\(\dfrac{42}{C_{DEF}}=\dfrac{2}{3}\)
=>\(C_{DEF}=42\cdot\dfrac{3}{2}=63\left(cm\right)\)
Ta có:
\(\Delta ABC\sim\Delta DEF\left(gt\right)\)
\(\Rightarrow\dfrac{C_{ABC}}{C_{DEF}}=k=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{42}{C_{DEF}}=\dfrac{2}{3}\Rightarrow C_{DEF}=63\) (cm)

Lời giải:
a. $\triangle A'B'C'\sim \triangle ABC$ theo tỉ số $k$
$\Rightarrow \frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=k$
$\Rightarrow A'B'=kAB; B'C'=kBC; C'A'=kCA$
$\Rightarrow A'B'+B'C'+C'A'=k(AB+BC+AC)$
$\Rightarrow P_{A'B'C'}=kP_{ABC}$
$\Rightarrow \frac{P_{A'B'C'}}{P_{ABC}}=k$
b.
Chu vi tam giác ABC:
$40:(5-3).3=60$ (dm)
Chu vi tam giác A'B'C':
$40:(5-3).5=100$ (dm)

Chọn C
C