
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


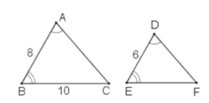
a, 2 tam giác đồng dạng
CM:
xét tam giác ta có: \(2x+3x+4x=56\)(\(x\)là hệ số sao cho \(2x;3x;4x\)là ba cạnh của tam giác ABC)
=) \(x=6\)
tỉ lệ cạnh thì cậu chứng minh đc 2 tam giác đồng dạng nhé
b,vì hai tam đồng dạng nên
\(\widehat{ABC}=\widehat{DEF}=45^O\)
\(\widehat{BAC}=\widehat{EDF}=105^O\)
tổng 3 góc trong tam giác =180o
thì tính đc \(\widehat{ACB}=\widehat{DFE}=30^O\)
sao khi ra x=6 nhân vào 2x=2.6=12=AB
3x=3.6=18=AC
BC=4x=4.6=24
tỉ lệ cạnh \(\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}\)
hay \(\frac{12}{3}=\frac{18}{4,5}=\frac{24}{6}\)

ΔABC đồng dạng với ΔDEF
=>AB/DE=BC/EF=AC/DF=k=1/3
=>3/DE=4/DF=1/3
=>DE=9cm; DF=12cm
ΔABC đồng dạng với ΔDEF
=>góc B=góc E=60 độ; góc C=góc F=30 độ
góc A=góc D=180-60-30=90 độ

a: ΔFME vuông tại M
=>MF^2+ME^2=EF^2
=>\(EF=\sqrt{9^2+6^2}=3\sqrt{13}\left(cm\right)\)
Xét ΔFME vuông tại M có
\(sinE=\dfrac{MF}{EF}=\dfrac{6}{3\sqrt{13}}=\dfrac{2}{\sqrt{13}}\)
\(cosE=\dfrac{ME}{EF}=\dfrac{3}{\sqrt{13}}\)
tan E=2/căn 13:3/căn 13=2/3
cot E=1:2/3=3/2
b: ΔDEF vuông tại F có FM là đường cao
nên FM^2=DM*ME
=>DM=6^2/9=4cm
DE=9+4=13cm
ΔDEF vuông tại F
=>FD^2+FE^2=ED^2
=>FD^2=13^2-(3căn 13)^2=169-117=52
=>FD=2căn 13(cm)
c: Xét ΔDMF vuông tại M có
sin D=FM/FD=6/2căn 13=3/căn 13
cos D=MD/DF=2/căn 13
tan D=3/căn 13:2/căn 13=3/2
cot D=1:3/2=2/3

a) Xét ΔDEF có
EM là đường phân giác ứng với cạnh DF(gt)
nên \(\dfrac{DM}{DE}=\dfrac{MF}{EF}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{DM}{5}=\dfrac{MF}{6}\)
mà DM+MF=DF(M nằm giữa D và F)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DM}{5}=\dfrac{MF}{6}=\dfrac{DM+MF}{5+6}=\dfrac{DF}{11}=\dfrac{5}{11}\)
Do đó:
\(\dfrac{DM}{5}=\dfrac{5}{11}\)
hay \(DM=\dfrac{25}{11}cm\)
Vậy: \(DM=\dfrac{25}{11}cm\)

Xét ΔABC có BM là đường phân giác
nên AM/AB=CM/CB
=>AM/3=CM/5
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AM}{3}=\dfrac{CM}{5}=\dfrac{AM+CM}{3+5}=\dfrac{4}{8}=\dfrac{1}{2}\)
Do đó: AM=1,5(cm)
Xét ΔABM vuông tại A và ΔDEF vuông tại D có
AB/DE=AM/DF
Do đó: ΔABM\(\sim\)ΔDEF


DE=8cm
DF=16cm