Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(BC=\sqrt{AB^2+AC^2}=\sqrt{16^2+12^2}=20\left(cm\right)\)
Ta có: \(AB.AC=AH.BC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12.16}{20}=\dfrac{48}{5}\left(cm\right)\)
Ta có: \(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{16^2}{20}=\dfrac{64}{5}\left(cm\right)\)
Ta có: \(sinB=\dfrac{AC}{BC}=\dfrac{12}{20}=\dfrac{3}{5}\Rightarrow\angle B\approx37\)
b) tam giác AHE vuông tại H có HN là đường cao \(\Rightarrow AN.AE=AH^2\)
tam giác ABC vuông tại A có AH là đường cao \(\Rightarrow AH^2=HB.HC\)
\(\Rightarrow AN.AE=HB.HC\)
c) tam giác AHB vuông tại H có HM là đường cao \(\Rightarrow AH^2=AM.AB\)
\(\Rightarrow AN.AE=AM.AB\Rightarrow\dfrac{AM}{AE}=\dfrac{AN}{AB}\)
Xét \(\Delta AMN\) và \(\Delta AEB:\) Ta có: \(\left\{{}\begin{matrix}\angle EABchung\\\dfrac{AM}{AE}=\dfrac{AN}{AB}\end{matrix}\right.\)
\(\Rightarrow\Delta AMN\sim\Delta AEB\left(c-g-c\right)\Rightarrow\dfrac{AE}{AM}=\dfrac{BE}{MN}\)
mà \(BE=3MN\Rightarrow\dfrac{BE}{MN}=3\Rightarrow\dfrac{AE}{AM}=3\Rightarrow AE=3AM\)
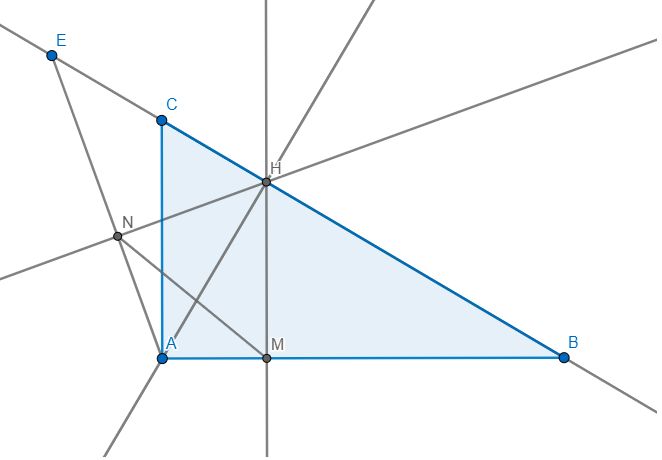

Sửa đề: ΔABC vuông tại A
a: MB/NH=BH^2/AB:CH^2/AC
=BH^2/CH^2*AC/AB
=(AB/AC)^4*AC/AB=AB^3/AC^3
b: BC*BM*CN
=BC*BH^2/AB*CH^2/AC
=AH^4/AH=AH^3
c: ΔAHB vuông tại H có HM là đường cao
nên AM*AB=AH^2
ΔAHC vuông tại H có HN là đường cao
nen AN*AC=AH^2
ΔABC vuông tại A có AH vuông góc BC
nên HB*HC=AH^2
=>HB*HC=AM*AB
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
=>AH=MN
=>AM*AB=HB*HC=MN^2
d: BM*BA+AN*AC
=BH^2+AH^2=AB^2=BH*BC

b: Xét ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB
nên \(\left\{{}\begin{matrix}AM\cdot AB=AH^2\left(1\right)\\AM\cdot MB=MH^2\end{matrix}\right.\)
Xét ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC
nên \(\left\{{}\begin{matrix}AN\cdot AC=AH^2\left(2\right)\\NA\cdot NC=NH^2\end{matrix}\right.\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
Xét tứ giác AMHN có
\(\widehat{NAM}=\widehat{ANH}=\widehat{AMH}=90^0\)
Do đó: AMHN là hình chữ nhật
Xét ΔHNM vuông tại H có
\(NM^2=HN^2+HM^2\)
hay \(HB\cdot HC=AM\cdot MB+AN\cdot NC\)

a, xét \(\Delta ABC\) vuông tại A áp dụng hệ thức lượng\(=>AC^2=CH.BC=>HC=\dfrac{AC^2}{BC}=\dfrac{12^2}{15}=9,6cm\)
\(=>HB=BC-HC=15-9,6=5,4cm\)
áp dụng Pytago trong \(\Delta AHC\) vuông tại H
\(=>HA=\sqrt{AC^2-HC^2}=\sqrt{12^2-9,6^2}=7,2cm\)
\(b,\) do E,F là hình chiếu vuông góc của H lần lượt lên AB, AC
\(=>\left\{{}\begin{matrix}EH\perp AB\\HF\perp AC\end{matrix}\right.\) mà \(\Delta AHB\) và \(\Delta AHC\) lần lượt vuông góc tại H
theo hệ thức lượng
\(=>\left\{{}\begin{matrix}AH^2=AE.AB\\AH^2=AF.AC\end{matrix}\right.\)=>\(AE.AB=AF.AC\)
c, do E,F là hình chiếu vuông góc của H lần lượt lên AB, AC
=> tứ giác EHFA là hình chữ nhật\(=>AE=HF< =>HF^2=AE^2\)
áp dụng pytago trong \(\Delta EHA\) vuông tại E
\(=>HE^2+AE^2=AH^2< =>HE^2+HF^2=AH^2\)(1)
theo hệ thức lượng trong tam giác ABC vuông tại A đường cao AH
\(=>AH^2=HB.HC\left(2\right)\)
(1)(2)=>\(HE^2+HF^2=HB.HC\)

a: Xét ΔBAC vuông tại A có
\(AC=6\cdot\sin60^0\)
hay \(AC=3\sqrt{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AB^2=9\)
hay AB=3cm
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9}{6}=1.5\left(cm\right)\\CH=\dfrac{27}{6}=4.5\left(cm\right)\end{matrix}\right.\)

a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=4\cdot6=24\)
=>\(AH=2\sqrt{6}\left(cm\right)\)
ΔAHC vuông tại H
=>\(HA^2+HC^2=AC^2\)
=>\(AC^2=24+36=60\)
=>\(AC=2\sqrt{15}\left(cm\right)\)
ΔAHB vuông tại H
=>\(AB^2=AH^2+HB^2=16+24=40\)
=>\(AB=2\sqrt{10}\left(cm\right)\)
b: BC=BH+CH=10cm
c: ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(1\right)\)
Xét ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=BK\cdot BM\)

a) AM.AB = AN.AC
△AHB vuông tại H, đường cao HM, △AHC vuông tại H, đường cao HN
⇒AM.AB = AN.AC = AH^2 (hệ thức về cạnh và đường cao...)
b) HB.HC = MA.MB + NA.NC
- Tam giác ABC vuông tại A, đường cao AH
suy ra HB.HC = AH^2 (hệ thức về cạnh và đường cao...)
mà tứ giác AMHN là hcn, suy ra AH(^2) = MN(^2)
- △AHB vuông tại H, đường cao HM, △AHC vuông tại H, đường cao HN
suy ra MA.MB + NA.NC = HM(^2) + (HN^2)= (MN^2)
từ đó suy ra điều phải c/m
c) (HB/HC)=((AB/AC))(^2)
((AB/AC))(^2)=((AB^2)/AC(^2)) = (BH.BC/CH.BC)=(HB/HC)
b: Xét ΔHAC vuông tại H có HN là đường cao
nên \(HA^2=AN\cdot AC\left(1\right)\)
Xét ΔHAB vuông tại H có HM là đường cao
nên \(HA^2=AM\cdot AB\left(2\right)\)
Từ (1) và (2) suy ra; \(AN\cdot AC=AM\cdot AB\)