Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔAMB và ΔAMC, ta có:
AB = AC (gt)
BM = CM (vì M là trung điểm BC)
AM cạnh chung
Suy ra: ΔAMB= ΔAMC(c.c.c)
⇒ ∠(AMB) =∠(AMC) ̂(hai góc tương ứng)
Ta có: ∠(AMB) +∠(AMC) =180o (hai góc kề bù)
∠(AMB) =∠(AMC) =90o. Vậy AM ⏊ BC
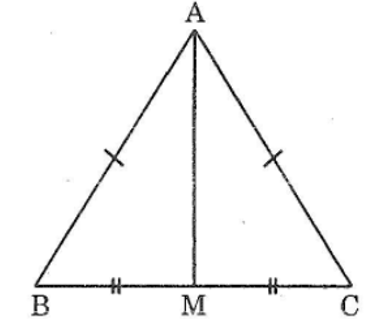
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nen AM là đường cao

a) Xét tam giác ABG và tam giác ACG, có:
BG=GC( G trung điểm BC)
AB=AC (gt)
AG: chung
Vậy tan giác ABG= tam giác ACG( c-c-c)
b) Ta có: Góc AGB+ góc AGC= 180° ( kề bù)
Mà góc AGC= góc AGB ( tam giác ABG= tam giác ACG)
Suy ra góc AGC= góc AGB = 180°: 2= 90°
Vậy AG vuông góc BC
c) Ta có: góc ABG+ góc GBD= 180° ( kề bù)
Góc ACG+ góc GCE= 180° ( kề bù )
Mà góc ABG= góc ACG ( tam giác ABG= tam giác ACG)
Vậy góc GBD= góc GCE
Xét tam giác BGD và tam giác CGE, có :
Góc DBG= góc ECG ( cmt)
BD= CE ( gt)
BG= GC ( G trung điểm BC)
Vậy tam giác BGD= tam giác CGE ( c-g-c)
Suy ra GD= GE ( 2 cạnh tương ứng)

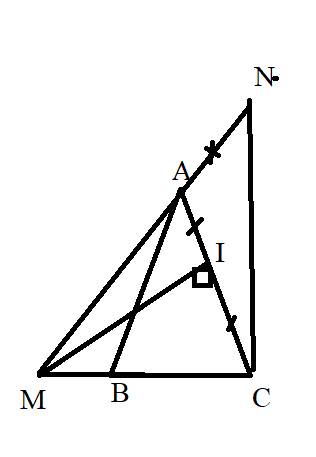
a: Xét ΔMAC có
MI là đường cao
MI là đường trung tuyến
Do đó: ΔMAC cân tại M
=>\(\widehat{AMC}=180^0-2\cdot\widehat{ACM}=180^0-2\cdot\widehat{ACB}\left(1\right)\)
ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ACB}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{AMC}=\widehat{BAC}\)
b:
ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\)
\(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
=>\(\widehat{ABM}=180^0-\widehat{ABC}=180^0-\widehat{ACB}\left(3\right)\)
\(\widehat{CAN}+\widehat{CAM}=180^0\)(hai góc kề bù)
=>\(\widehat{CAN}+\widehat{ACB}=180^0\)
=>\(\widehat{CAN}=180^0-\widehat{ACB}\left(4\right)\)
Từ (3) và (4) suy ra \(\widehat{ABM}=\widehat{CAN}\)
Xét ΔABM và ΔCAN có
AB=CA
\(\widehat{ABM}=\widehat{CAN}\)
BM=AN
Do đó;ΔABM=ΔCAN
c: ΔABM=ΔCAN
=>NC=MA
mà MA=MC
nên NC=MC
\(\widehat{AMC}=\widehat{BAC}\)
mà \(\widehat{BAC}=45^0\)
nên \(\widehat{AMC}=45^0\)
Xét ΔCMN có CM=CN và \(\widehat{CMN}=45^0\)
nên ΔCMN vuông cân tại C