Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

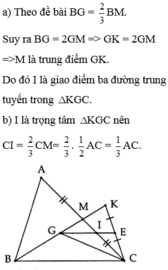
a) Ta có : MK = GK - GM = BG - 1/2 BG = 1/2BG = 1/2GK
=> M là trung điểm GK
Ta thấy tam giác KGC có 2 dg trung tuyến CM và GE cắt nhau tại I
=> I là trọng tâm tam giác KGC
b) Do I là trọng tâm tam giác KGC nên CI = 2/3MC
Mà MC = 1/2AC
=> CI = 1/3AC

a) Ta có:MK=GK-GM=BG-1/2BG=1/2BG=1/2GK=>M là trung điểm GK
Xét \(\Delta\)KGC có 2 đường trung tuyến là CM và GE cắt nhau tại I
=> I là trọng tâm của \(\Delta\)KGC
b)Do I là trọng tâm của \(\Delta\)KGC
Nên: CI=2/3MC
Mà: MC=1/2AC
Suy ra: CI=1/3AC

a) BM là trung tuyến của tam giác ABC, G thuộc BM, BG=2/3BM => G la trọng tâm của tam giác ABC
=> GM=1/2BG
G là trung điểm của BK => GK=BG => GM+MK=BG. GM=1/2BG => 1/2BG+MK=BG => MK=1/2BG
=> GM=MK=1/2BM
Xét tam giác GKC: M trung điểm của GK, N là trung điểm của KC
=> CM và GN là trung tuyến của tam giác GKC. Mà CM, GN cắt nhau tại O
=> O là trọng tâm của tam giác GKC (đpcm)
b) GN là trung tuyển, O là trọng tâm => GO=2/3GN (1)
Xét tam giác BKC: G là trung điểm BK, N là trung điểm KC => GN=1/2BC (T/c đường trung bình) (2)
(1);(2) => GO=\(\dfrac{2}{3}.\dfrac{1}{2}=\dfrac{1}{3}\) BC (đpcm)