Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


O là tâm đường tròn ngoại tiếp tam giác ABC nên ta vẽ đường kính AOE
Tứ giác BHCE là hình bình hành
M là trung điểm của BC. Do đó M là trung điểm của HE.
Kết hợp với O là trung điểm của AE suy ra OM là đường trung bình của \(\Delta AHE\)
\(\Rightarrow OM=\frac{1}{2}AH\)hay 2OM = AH
Vậy khoảng cách từ trực tâm tới đỉnh bằng 2 lần khoảng cách từ giao điểm các đường trung trực tới cạnh đối diện đỉnh đó (đpcm)


Vẽ đường kính BK của đường tròn tâm O ngoại tiếp tam giác ABC=> O trung điểm BK
Gọi M là chân đường vuông góc hạ từ O xuống dây BC => OM là khoảng cách từ O tới BC
Có OB=OC và B,C nằm trên đường tròn tâm O=> tam giác OBC cân tại O, đường cao OM=> M trung điểm BC
=> OM là đường trung bình tam giác BCK=> \(OM=\frac{1}{2}CK\)
C thuộc đường tròn đường kính BK=> tam giác BCK vuông tại K=> \(KC\perp BC\)
Mà \(AH\perp BC\Rightarrow AH//CK\)
A thuộc đường tròn đường kính BK=> tam giác BAK vuông tại A=> \(AK\perp AB\)
Mà \(CH\perp AB\Rightarrow CH//AK\)
=> AHCK là hình bình hành => \(AH=CK\Rightarrow OM=\frac{1}{2}AH\)

a) vì CD LÀ ĐƯỜNG KÍNH => GÓC DAC=90 (CHẮN NỬA ĐT) <=> DA VUÔNG GÓC AC. MÀ BH VUÔNG GÓC AC <=> DA//BH
TƯƠNG TỰ CHỨNG MINH AH //DB => ABDH LÀ HBH
B) gọi khoảng cách TỪ O ĐẾN BC LÀ OI VỚI OI VUÔNG GÓC BC.
TỪ QUAN HỆ ĐƯỜNG KÍNH VÀ DÂY => I LÀ TRUNG ĐIỂM BC
O LÀ TRUNG ĐIỂM CD => OI LÀ ĐTB CẢU TAM GIÁC CDB => OI=\(\frac{CD}{2}\)
MÀ CD=AH(HÌNH BÌNH HÀNH) => ĐIỀU PHẢI CM

a)
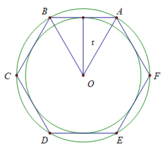
b) Cách vẽ lục giác đều có tất cả các đỉnh nằm trên đường tròn (O)
Vẽ các dây cung AB = BC = CD = DE = EF = FA = R = 2 cm
(Ta đã nêu được cách chia đường tròn thành sáu cung bằng nhau tại bài tập 10 SGK trang 71)
c) Vì các dây cung AB = BC = CD = DE = EF = FA bằng nhau nên khoảng cách từ O đến các dây là bằng nhau ( định lý liên hệ giữa dây cung và khoảng cách từ tâm đến dây)

Câu 1:
Xét ΔABC vuông tại A có
\(tanB=\dfrac{AC}{AB}\)
=>\(\dfrac{AC}{6}=\dfrac{4}{3}\)
=>\(AC=\dfrac{4}{3}\cdot6=8\left(cm\right)\)
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Câu 4:
a: Thay x=2 và y=5 vào y=(2m-1)x+3, ta được:
2(2m-1)+3=5
=>2(2m-1)=2
=>2m-1=1
=>2m=2
=>\(m=\dfrac{2}{2}=1\)
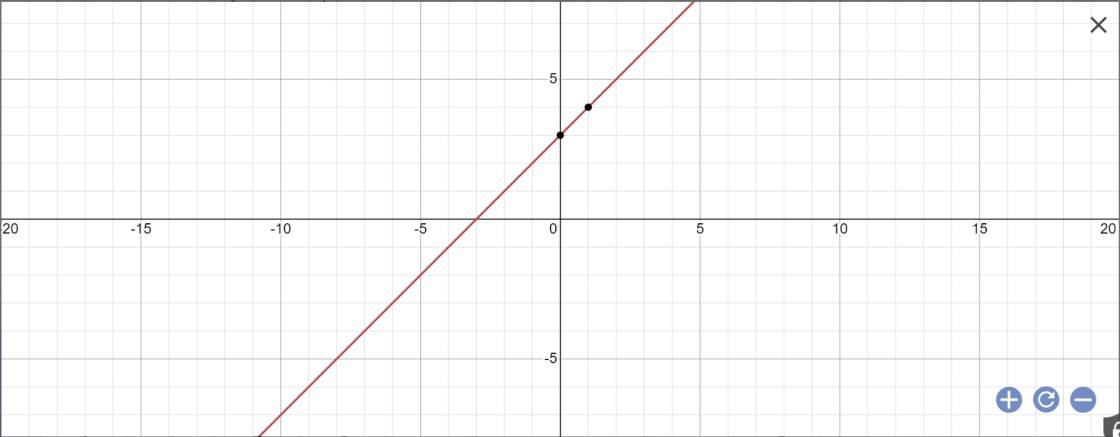
b: Khi m=1 thì \(y=\left(2\cdot1-1\right)x+3=x+3\)

Đáp án B.
Trong một đường tròn: Hai dây cách đều tâm thì bằng nhau

Chọn đáp án B.
Trong một đường tròn: Hai dây cách đều tâm thì bằng nhau
Câu hỏi của marivan2016 - Toán lớp 9 - Học toán với OnlineMath
Tham khảo nha!