K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

2 tháng 3 2021
Dễ thôi:vvv
a) Vì DF//AC
=> \(\dfrac{AF}{AB}=\dfrac{CD}{BC}=\dfrac{2}{1+2}=\dfrac{2}{3}\)
Vì DE//AB
=> \(\dfrac{AE}{AC}=\dfrac{BD}{BC}=\dfrac{1}{1+2}=\dfrac{1}{3}\)
b) Ta có: \(\dfrac{AE}{AC}=\dfrac{1}{3}\Leftrightarrow\dfrac{AE}{2AM}=\dfrac{1}{3}\Leftrightarrow\dfrac{AE}{AM}=\dfrac{2}{3}\)
Lại có: \(\dfrac{AF}{AB}=\dfrac{2}{3}\)
=> \(\dfrac{AF}{AB}=\dfrac{AE}{AM}\)
=> EF//BM(theo đ/lý Ta-lét đảo)

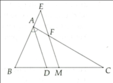
a) Xét \(\Delta MAP\)và \(\Delta MDI\)có:
\(\widehat{AMP}=\widehat{DMI}\)(đối đỉnh)
\(AM=DM\)(gt)
\(\widehat{MAP}=\widehat{MDI}\) (slt do DI // AC)
suy ra: \(\Delta MAP=\Delta MDI\) (g.c.g)
\(\Rightarrow\)\(AP=DI\)
\(\Delta BPC\)có: \(DI//PC\) ; \(DB=DC\)
\(\Rightarrow\)\(IB=IP\)
\(\Rightarrow\)\(DI\)là đường trung bình \(\Delta BPC\)
\(\Rightarrow\)\(DI=\frac{1}{2}PC\)
mà \(DI=AP\) (cmt)
\(\Rightarrow\)\(AP=\frac{1}{2}PC\)
\(\Rightarrow\)\(\frac{AP}{AC}=\frac{1}{3}\) (1)
b) Kẻ \(DK//AB\) \(\left(K\in QC\right)\)
Xét \(\Delta MAQ\)và \(\Delta MDK\)có:
\(\widehat{QMA}=\widehat{KMD}\)(đối đỉnh)
\(AM=DM\)(gt)
\(\widehat{QAM}=\widehat{KDM}\) (slt do KD // AQ)
suy ra: \(\Delta MAQ=\Delta MDK\) (g.c.g)
\(\Rightarrow\)\(AQ=DK\)
\(\Delta CBQ\)có \(DK//BQ\); \(DB=DC\)
\(\Rightarrow\)\(KQ=KC\)
\(\Rightarrow\)\(DK\)là đường trung bình \(\Delta CBQ\)
\(\Rightarrow\)\(\frac{DK}{BQ}=\frac{1}{2}\)
mà \(AQ=DK\)(cmt)
\(\Rightarrow\)\(\frac{AQ}{BQ}=\frac{1}{2}\)
\(\Rightarrow\)\(\frac{AQ}{AB}=\frac{1}{3}\) (2)
Từ (1) và (2) suy ra: \(PQ//BC\)
c) \(PQ//BC\)
\(\Rightarrow\)\(\Delta MQP~\Delta MCB\)
\(\Rightarrow\)\(\frac{PQ}{BC}=\frac{MP}{BM}\)
\(\Rightarrow\)\(PQ.BM=MP.BC\) (có lẽ đề sai)
cảm ơn bạn nhiều