Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta ABD\)có \(\widehat{A}\)tù \(\Rightarrow BA< BD\)(1); \(\widehat{ADB}< 90^o\)
\(\Rightarrow\widehat{BDE}>90^o\)\(\Rightarrow\Delta BDE\)tù tại D \(\Rightarrow BD< BE\)(2); \(\widehat{BED}< 90^o\)
\(\Rightarrow\widehat{BEC}>90^o\)\(\Rightarrow\Delta BEC\)tù tại E \(\Rightarrow BE< BC\)(3)
Từ (1), (2), (3) \(\Rightarrow BA< BD< BE< BC\left(đpcm\right)\)

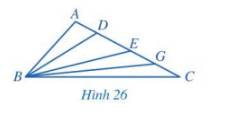
Xét tam giác BAD:
+ Góc A tù (góc > 90°) nên cạnh BD là cạnh lớn nhất trong tam giác này (đối diện với góc A).
Nên BD > BA.
+ Góc A tù nên góc ABD và góc ADB là góc nhọn → góc BDE là góc tù (ba điểm A, D, E thẳng hàng hay góc ADE =180°). Vậy BE (đối diện với góc BDE) > BD.
Tương tự, ta có:
+ Góc BDE là góc tù nên góc DBE và góc DEB là góc nhọn → góc BEG là góc tù. Vậy BG > BE.
+ Góc BEG là góc tù nên góc EBG và góc EGB là góc nhọn → góc BGC là góc tù. Vậy BC > BG.
Vậy BA < BD <BE < BG < BC.
Hay các đoạn thẳng BA, BD, BE, BG, BC theo thứ tự tăng dần là: BA, BD, BE, BG, BC.

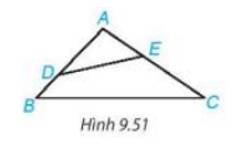
Ta có \(\widehat {BAC}\) là góc tù nên \(\widehat {ADE},\widehat {AED}\) là các góc nhọn
\( \Rightarrow \widehat {DEC}\) là góc tù
\( \Rightarrow DE < DC\) (quan hệ giữa góc và cạnh đối diện trong tam giác DEC). (1)
Xét tam giác ADC có:
\(\widehat {DAC}\) là góc tù nên \(\widehat {ADC},\widehat {ACD}\) là các góc nhọn
\( \Rightarrow \widehat {BDC}\) là góc tù.
\( \Rightarrow DC < BC\) (quan hệ giữa góc và cạnh đối diện trong tam giác BDC) (2)
Từ (1) và (2) suy ra: BC > DE

Giải thích các bước giải:
a)Xét tam giác BAD và tam giác BED:
BD:cạnh chung
^ABD=^EBD (vì BD là tia phân giác của ^ABC)
AB=BE(gt)
=>tam giác BAD=tam giác BED(c.g.c)
b)Từ tam giác BAD=tam giác BED(cmt)
=>AD=DE(cặp cạnh t.ứ)
và ^BAD=^BED(cặp góc .tứ),mà ^BAD=900 (^BAC=900)=>^BED=900
Xét tam giác DFA vuông ở A và tam giác DCE vuông ở E có:
AD=AE (cmt)
^ADF=^EDC (2 góc đối đỉnh)
=>tam giác DFA=tam giác DCE(cgv-gnk)
=>DF=DC(cặp cạnh t.ứ)
=>tam giác DFC cân tại D (dấu hiệu nhận biết tam giác cân)
c)Từ tam giác DFA=tam giác DCE (cmt)
=>AF=CE(cặp cạnh t.ứ)
Ta có: BE+CE=BC
BA+AF=BF
mà AF=CE(cmt),AB=AE(gt)
=>BC=BF
=>tam giác BFC cân tại B (dấu hiệu nhận biết tam giác cân)
=>^BCF=1800−FBC21800−FBC2 (tính chất tam giác cân) (1)
Vì AB=AE(gt)
=>tam giác ABE cân tại B (dấu hiệu nhận biết tam giác cân)
=>^BEA=1800−ABE21800−ABE2 (tính chất tam giác cân) (2)
Từ (1);(2);lại có ^ABE=^FBC
=>^BCF=^BEA,mà 2 góc này nằm ở vị trí đồng vị
=>AE//CF(dấu hiệu nhận biết 2 đg thẳng song song)

4) a.Ta có:
\(BA=BE\)
\(ABD=DBE\rightarrow\Delta ABD=\Delta EBDchungBD\)
b) Từ câu a \(\rightarrow BED=BAD=90^o\)
\(\rightarrow DE\text{⊥}BC\)
c) Ta có :
\(BKD=ADK=ACB+DEC=90^o\)
\(BKD=ACB\)
\(\text{Δ B D K = Δ B D C ( g . c . g )}\)
\(BK=BC\)

5)
Ta có:
\(2^{300}=\left(2^3\right)^{100}=8^{100}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}\)
Mà \(8< 9\Rightarrow2^{300}< 3^{200}\)
Bài 5:
\(2^{300}=\left(2^3\right)^{100}=8^{100}\\ 3^{200}=\left(3^2\right)^{100}=9^{100}\\ Vì:8< 9\Rightarrow8^{100}< 9^{100}\\ \Rightarrow2^{300}< 3^{200}\)

a.Ta có:
⎧⎪⎨⎪⎩BA=BEˆABD=ˆDBEchungBD→ΔABD=ΔEBD(c.g.c){BA=BEABD^=DBE^chungBD→ΔABD=ΔEBD(c.g.c)
b.Từ câu a→ˆBED=ˆBAD=90o→BED^=BAD^=90o
→DE⊥BC→DE⊥BC
c.Ta có:
ˆBKD+ˆADK=ˆACB+ˆDEC=90oBKD^+ADK^=ACB^+DEC^=90o
→ˆBKD=ˆACB→BKD^=ACB^
→ΔBDK=ΔBDC(g.c.g)→ΔBDK=ΔBDC(g.c.g)
→BK=BC→BK=BC


a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔBAD=ΔBED
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE\(\perp\)BC
c: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: AK=EC
Ta có: BA+AK=BK
BE+EC=BC
mà BA=BE
và AK=EC
nên BK=BC