Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác ABEC có
O là trung điểm của BC
O là trung điểm của AE
Do đó: ABEC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABEC là hình chữ nhật

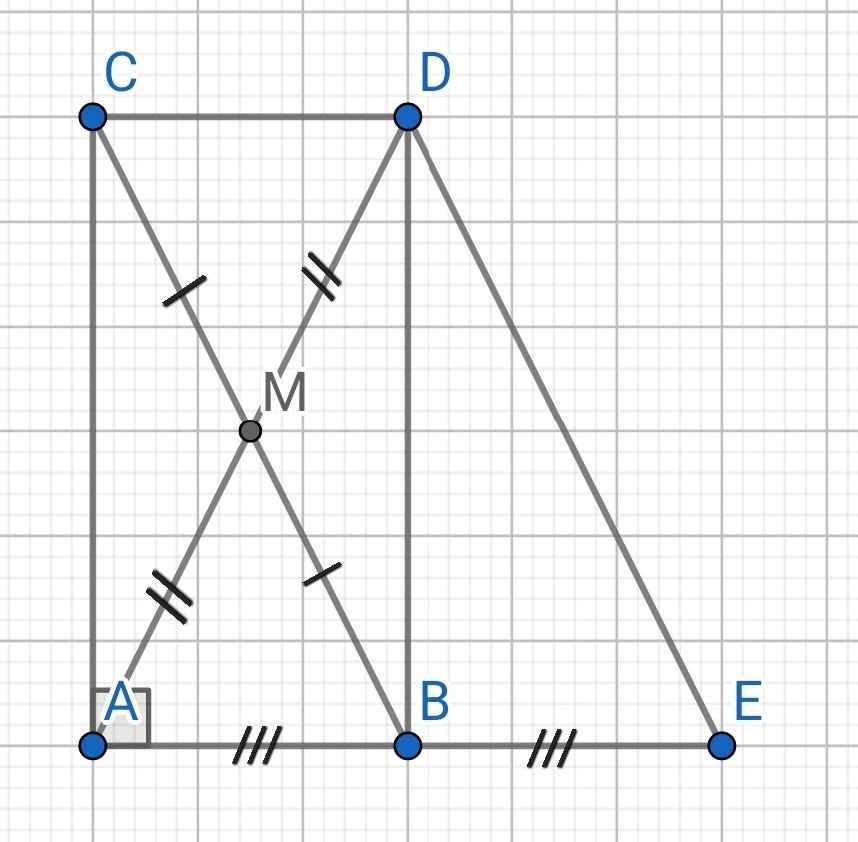 a) Tứ giác ABDC có:
a) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ABDC là hình chữ nhật
b) Do ABDC là hình chữ nhật (cmt)
⇒ CD = AB (1)
Do B là trung điểm của AE (gt)
⇒ BE = AB = AE : 2 (2)
Từ (1) và (2) ⇒ CD = BE
Do ABDC là hình chữ nhật (cmt)
⇒ CD // AB
⇒ CD // BE
Tứ giác BEDC có:
CD // BE (cmt)
CD = BE (cmt)
⇒ BEDC là hình bình hành
c) Do ABDC là hình chữ nhật (cmt)
⇒ AC // BD
Do đó AC, BD, EK đồng quy là vô lý
Em xem lại đề nhé!

Xét tứ giác ABDC có
O là trung điểm của BC
O là trung điểm của AD
Do đó: ABDC là hình bình hành

a) Xét ∆CMA và ∆BMD:
Góc CMA= góc BMD (đối đỉnh)
MA=MD (gt)
MC=MB (M là trung điểm BC)
=> ∆CMA=∆BMD(c.g.c)
=> góc CAM = góc BDM và CA=DB
Mà 2 góc CAM và góc BDM nằm ở vị trí so lo trong nên CA//DB
=> CABD là hình bình hành
Lại có góc CAB = 90 độ (gt)
=> ACDB là hình chữ nhật
b) Vì E là điểm đối xứng của C qua A nên EAB=90độ=DBA
Mà 2 góc này ở bị trí so le trong nên AE//DB
Lại có AE=BD(=CA)
=> AEBD là hình bình hành

a: Xét tứ giác ABNC có
O là trung điểm chung của AN và BC
=>ABNC là hình bình hành
Hình bình hành ABNC có \(\widehat{BAC}=90^0\)
nên ABNC là hình chữ nhật
b: CN//AB
\(C\in\)DN
Do đó: CD//AB
CN=AB
CN=CD
Do đó: AB=CD
Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó: ABCD là hình bình hành

a: Xét tứ giác AHBD có
O là trung điểm chung của AB và HD
=>AHBD là hình bình hành
Hình bình hành AHBD có \(\widehat{AHB}=90^0\)
nên AHBD là hình chữ nhật
b: Ta có: AHBD là hình chữ nhật
=>AH//BD và AH=BD
Ta có: AH//BD
Q\(\in\)AH
Do đó: QH//DB
Ta có: AH=BD
AH=HQ
Do đó: BD=HQ
Xét tứ giác BDHQ có
BD//HQ
BD=HQ
Do đó: BDHQ là hình bình hành
c: Xét tứ giác ABQP có
H là trung điểm chung của AQ và BP
=>ABQP là hình bình hành
Hình bình hành ABQP có AQ\(\perp\)BP
nên ABQP là hình thoi
d: Ta có: ΔKAB vuông tại K
mà KO là đường trung tuyến
nên \(KO=\dfrac{AB}{2}\)
mà AB=HD(AHBD là hình chữ nhật)
nên \(KO=\dfrac{HD}{2}\)
Xét ΔKHD có
KO là đường trung tuyến
\(KO=\dfrac{HD}{2}\)
Do đó: ΔKHD vuông tại K
=>KH\(\perp\)KD

\(a,\) Vì M là trung điểm AB cà DH nên AHBD là hình bình hành
Mà \(\widehat{AHB}=90^0\) (đường cao AH) nên AHBD là hcn
\(b,\) Vì AHBD là hcn nên \(AD=BH;AD\text{//}HB\)
Mà \(BH=HE\Rightarrow AD=HE;AD\text{//}HE\)
Do đó: ADHE là hình bình hành
\(c,\) Vì ADHE là hbh mà N là giao AH và DE nên N là trung điểm AH và DE
Mà M là trung điểm AB nên MN là đtb \(\Delta ABH\)
Do đó \(MN//BH\) hay \(MN//BC\)
Ta có N là trung điểm AH và K là trung điểm AC nên NK là đtb \(\Delta ACH\)
Do đó \(NK//HC\) hay \(NK//BC\)
Do đó theo định lí Ta lét thì MN trùng NK hay M,N,K thẳng hàng
a: Xét tứ giác AHBD có
M là trung điểm của AB
M là trung điểm của HD
Do đó: AHBD là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBD là hình chữ nhật



Mng trl giúp e vs ạ
Xét tứ giác ACEB có
O là trung điểm của AE
O là trung điểm của BC
Do đó: ACEB là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ACEB là hình chữ nhật