
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


tự vẽ hình:::::
áp dụng định lí py-ta-go vào tam giác BHA vuông tại H ta được:
BH2+AH2=AB2(1)
áp dụng định lí py-ta-go vào tam giác AHC vuông tại H ta được:
HC2+AH2=AC2(2)
áp dụng định lí py-ta-go vào tam giác ABC vuông tại A ta được:
AB2+AC2=BC2(3)
Công hai vế (1);(2) kết hợp với (3) ta được:
HB2+HC2+AH2+AH2=AB2+AC2
92+162+2AH2=BC2
337+2AH2=(9+16)2
2AH2=625-337
2AH2=288
AH2=144
=>AH=√144=12(cm)
bạn ơi ko phải mk ko giúp mà về phần hình học mình dốt lắm

Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng hệ thức : AH^2 = HB . HC = 16 . 9
=> AH = 4 . 3 = 12 cm

Bạn tự vẽ hình ra hì. Mình vẽ ko được
Bài làm
Tam giác AHB vuông tại H: AH^2+HB^2=AB^2
Tam giác AHC vuông tại H:AH^2+HC^2=AC^2
Tam giác ABC vuông tại A:BC^2=AB^2+AC^2
BC=HB+HC=9+16=25
BC^2=AH^2+HB^2+AH^2+HC^2=2AH^2+HB^2+HC^2=25^2=625
2HA^2+9^2+16^2=625
2HA^2+337=625
2HA^2=288
HA^2=144
HA=12

`Answer:`
Có `BC=HB+HC=9+16=25cm`
Áp dụng định lý Pytago vào `\triangleABC` vuông tại `A=>BC^2=AB^2+AC^2(1)`
Áp dụng định lý Pytago vào `\triangleAHB` vuông tại `H=>AB^2=HB^2+AH^2(2)`
Áp dụng định lý Pytago vào `\triangleAHC` vuông tại `H=>AC^2=HC^2+AH^2(3)`
Từ `(1)(2)(3)=>AB^2+AC^2=HB^2+HC^2+AH^2+AH^2`
`=>BC^2=9^2+16^2+2AH^2`
`=>25^2=81+256+2AH^2`
`=>625 = 337 + 2AH²`
`=>2AH² = 625 - 337 = 288`
`=>AH^2=144`
`=>AH=\sqrt{144}=12cm`

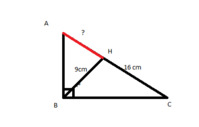
A B C H 9cm 16cm AH=?
Chứng minh:
Xét \(\Delta ABC\) vuông tại A , có:
AH là đường cao (\(H\in BC\)).
Ta lại có: BC= BH + HC = 9 + 16 = 25 (cm). -> (1)
\(\Delta ABC\) vuông tại A => BC là cạnh huyền -> (2)
Từ (1) và (2) => \(AH=\frac{1}{2}BC=\frac{25}{2}=12,5\left(cm\right)\) (tính chất đường cao của tam giác vuông).


BC=9+16=25(cm)
tam giác AHB_|_ tại H
áp dụng định lí py-ta-go, ta có:
\(AH^2=AB^2-HB^2=AB^2-9^2=AB^2-81\left(1\right)\)
tam giác AHC vuông tại H
\(\Rightarrow AH^2=AC^2-CH^2=AC^2-16^2=AC^2-256\left(2\right)\)
từ (1)(2) suy ra :\(AH^2+AH^2=AB^2-81+AC^2-256\)
\(\Rightarrow2.AH^2=\left(AB^2+AC^2\right)-81-256\)
\(\Rightarrow2.AH^2=BC^2-337\)( vì tam giác ABC vuông tại A nên AB^2+AC^2=BC^2)
\(\Rightarrow2.AH^2=25^2-337=625-337=288\)
\(\Rightarrow AH^2=288:2=144\)
\(\Rightarrow AH=\sqrt{144}=12\left(cm\right)\)
thiếu đề kìa, phần thiếu là kẻ AH_|_BC tại H ak