Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Ta có: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
Ta có: AB//CD
AB\(\perp\)AC
Do đó: CD\(\perp\)CA
Xét ΔABC vuông tại A và ΔCDA vuông tại C có
AB=CD
AC chung
Do đó: ΔABC=ΔCDA
c: Ta có: ΔABC=ΔCDA
=>BC=DA
Xét ΔMCA và ΔMBD có
MC=MB
\(\widehat{CMA}=\widehat{BMD}\)(hai góc đối đỉnh)
MA=MD
Do đó: ΔMCA=ΔMBD
=>\(\widehat{MCA}=\widehat{MBD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
Ta có: AC//BD
AC\(\perp\)CD
Do đó: DC\(\perp\)DB
=>ΔDBC vuông tại D

a, xét tam giác AMB và tam giác DMC có : MA = MD (gt)
MC = MB do M là trung điểm của BC (gt)
góc DMC = góc BMA (đối đỉnh)
=> tam giác AMB = tam giác DMC (c-g-c)
b, tam giác AMB = tam giác DMC (câu a)
=> góc DCM = góc MAB (đn) mà 2 góc này so le trong
=> DC // AB (đl)
c,
https://olm.vn/thanhvien/cuongktl
SÉT \(\Delta AMC\)VÀ\(\Delta DMB\)CÓ
\(AM=DM\left(gt\right)\)
\(\widehat{AMC}=\widehat{DMB}\left(đđ\right)\)
\(MC=MB\left(gt\right)\)
\(\Rightarrow\Delta AMC=\Delta DMB\left(C-G-C\right)\)
TA CÓ\(\Delta MAB+\Delta AMC=\Delta ABC\)
\(\Delta DMB+\Delta MDC=\Delta DCB\)
MÀ \(\Delta AMC=\Delta DMB\left(cmt\right)\)
\(\Delta MAB=\Delta MDC\left(cmt\right)\)
\(\Rightarrow\Delta ABC=\Delta DCB\)
\(\Rightarrow\widehat{A}=\widehat{D}=90^o\)(HAI GÓC TƯƠNG ỨNG)
VẬY \(\Delta BDC\)TAM GIÁC VUÔNG TẠI D

a/ Xét △ABM và △DMC có:
\(\begin{matrix}AM=MD\left(gt\right)\\MB=MC\left(gt\right)\\\hat{AMB}=\hat{CMD}\left(đối\text{ }đỉnh\right)\end{matrix}\)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\) (đpcm).
b/ Ta có: \(\Delta AMB=\Delta DMC\left(cmt\right)\)
\(\Rightarrow\hat{MAB}=\hat{MDC}\); hai góc ở vị trí so le trong.
Vậy: AB // CD (đpcm).
c/ Xét △BAE có:
\(\begin{matrix}BH\perp AE\left(gt\right)\\AH=HE\left(gt\right)\end{matrix}\)
⇒ BH vừa là đường cao, vừa là đường trung tuyến.
⇒ △BAE cân tại B.
\(\Rightarrow BE=BA\). Mà \(AB=CD\left(\Delta AMB=\Delta DMC\right)\)
Vậy: BE = CD (đpcm).

a: Xét ΔAMC và ΔDMB có
MC=MB
\(\widehat{AMC}=\widehat{DMB}\)
MA=MD
DO đó: ΔAMC=ΔDMB
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: ΔABD vuông
c: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=BC/2

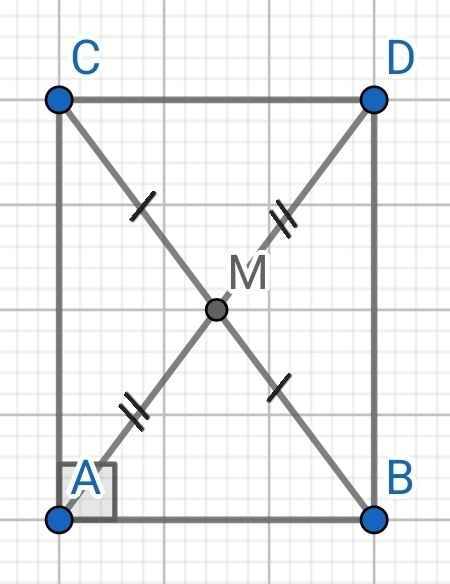
a) Do M là trung điểm của BC (gt)
⇒ MB = MC
Xét ∆AMB và ∆DMC có:
AM = DM (gt)
∠AMB = ∠DMC (đối đỉnh)
MB = MC (cmt)
⇒ ∆AMB = ∆DMC (c-g-c)
⇒ ∠MAB = ∠MDC (hai góc tương ứng)
Lại có:
∠MAC + ∠MAB = 90⁰ (∆ABC vuông tại A)
⇒ ∠MAC + ∠MDC = 90⁰
⇒ ∠DAC + ∠ADC = 90⁰
∆CDA có:
∠DAC + ∠CDA + ∠ACD = 180⁰ (tổng ba góc trong ∆ACD)
⇒ ∠ACD = 180⁰ - (∠DAC + ∠CDA)
= 180⁰ - 90⁰
= 90⁰
⇒ ∆ACD vuông tại C
Do ∆AMB = ∆DMC (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ABC và ∆CDA có:
AC là cạnh chung
AB = CD (cmt)
⇒ ∆ABC = ∆CDA (hai cạnh góc vuông)
b) Do ∆ABC = ∆CDA (cmt)
⇒ BC = AD (hai cạnh tương ứng)
Do AM = DM (gt)
⇒ AM = DM = ½AD
Mà AD = BC (cmt)
⇒ AM = ½BC
a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
DO đó: ABDC là hình bình hành
Suy ra: AB=DC; AC=BD
Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
Do đó: ΔABC=ΔCDA
b: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=1/2BC
*Tự vẽ hình
a) Xét tam giác MAB và MDC có :
MA=MD(GT)
BM=CM(GT)
\(\widehat{BMA}=\widehat{DMC}\left(đđ\right)\)
=> Tam giác MAB=MDC ( c.g.c )
b) Mình nghĩ đề bài sửa thành CM AB//CD thì có vẻ đúng hơn
Có : Tam giác MAB=MDC (cmt)
=> \(\widehat{BAD}=\widehat{ADC}\)
Mà 2 góc này ở vị trí so le trong
=> AB//CD
- Xét tam giác ABD và CDA có :
AD-cạnh chung
\(\widehat{ADC}=\widehat{DAB}\left(tgMAB=MDC\right)\)
AB=BC(tgMAB=MDC)
=> 2 tam giác này bằng nhau
c) Vâng, như đề bài thì chúng ta đã có tam giác ABC vuông tại A nên khỏi cần chứng minh đâu :)
#Hoctot