Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

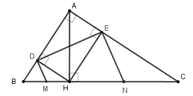
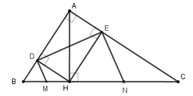
a: Xét tứ giác ADHE có
\(\widehat{EAD}=\widehat{ADH}=\widehat{AEH}=90^0\)
Do đó: ADHE là hình chữ nhật
a: Xét tứ giác ADHE có góc ADH=góc AEH=góc EAD=90 độ
nên ADHE là hình chữ nhật
=>DE=AH=6cm
b: Gọi O là giao của AH và DE
=>O là trung điểm chung của AH và DE
mà AH=DE
nên OA=OH=OD=OE
Ta có: góc OHD+góc MHD=90 độ
góc ODH+góc MDH=90 độ
mà góc OHD=góc ODH
nên góc MHD=góc MDH
=>ΔMHD cân tại M và góc MDB=góc MBD
=>ΔMBD cân tại M
=>MH=MB
=>M là trung điểm của HB
Cm tương tự, ta được N là trung điểm của HC
=>MN=1/2BC
d: \(AD\cdot AB=AH^2\)
\(AE\cdot AC=AH^2\)
Do đó: \(AD\cdot AB=AE\cdot AC\)

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=6\left(cm\right)\\CA=2\sqrt{13}\left(cm\right)\end{matrix}\right.\)

Tứ giác AEHD là hình chữ nhật vì: A ^ = E ^ = D ^ = 90 o nên DE = AH.
Xét ABC vuông tại A có: A H 2 = HB.HC = 9.16 = 144 => AH = 12
Nên DE = 12cm
Đáp án cần chọn là: A

Tứ giác ARHD là hình chữ nhật vì: A ^ = E ^ = D ^ = 90 ∘ nên DE = AH.
Xét ∆ ABC vuông tại A có A H 2 = HB.HC = 4.9 = 36 ⇔ AH = 6
Nên DE = 6cm
Đáp án cần chọn là : D