Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Ta có: góc B + góc C = 90 độ
Mà góc B = 50 độ
\(\Rightarrow\) góc C = 90 độ - 50 độ = 40 độ
b)
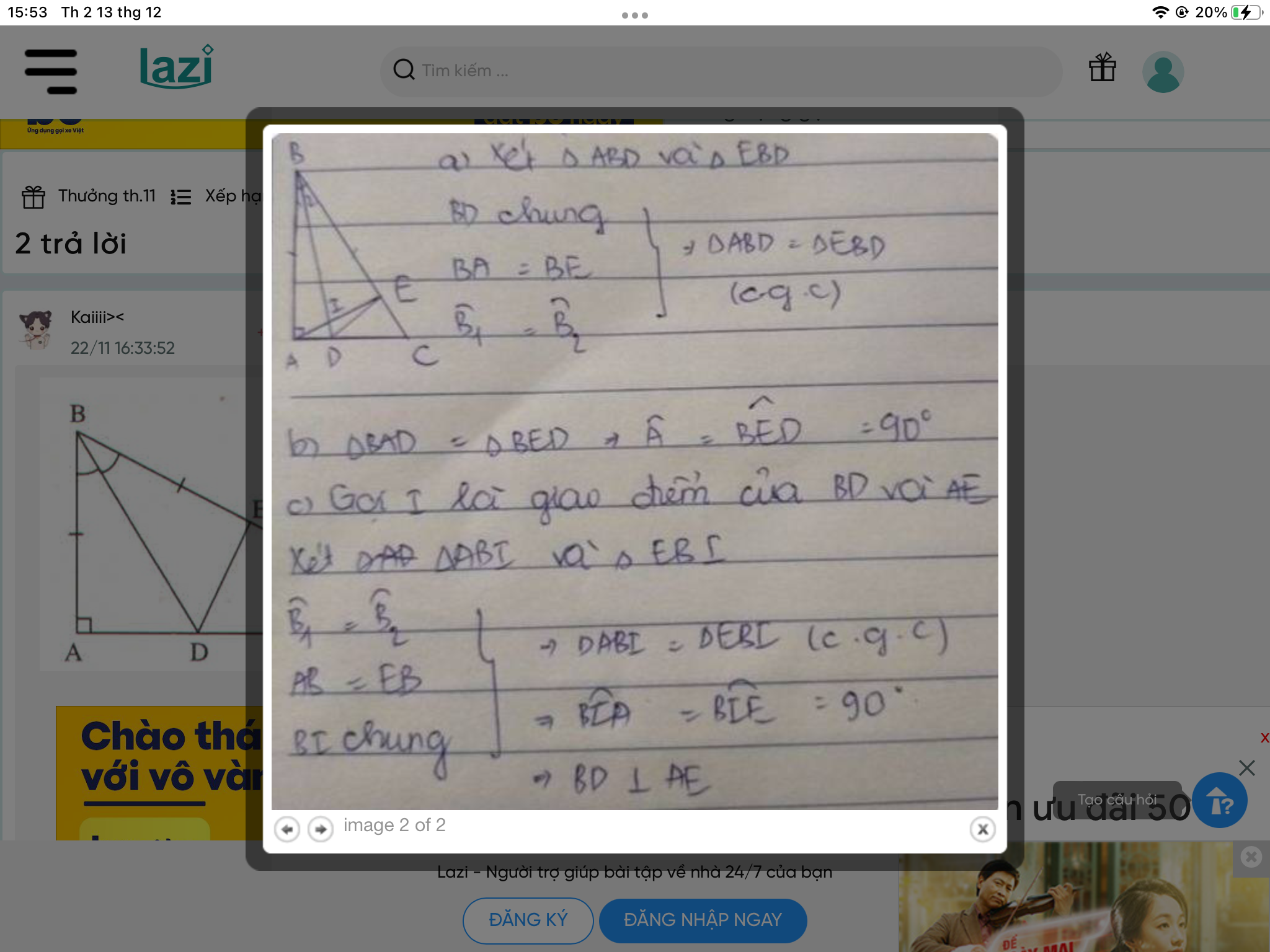
Xét Δ ABD và Δ EBD có:
AB = EB (gt)
góc ABD = góc EBD (gt)
chung BD
\(\Rightarrow\) Δ ABD = Δ EBD (c-g-c)
c)
Vì Δ ABD = Δ EBD (câu b)
\(\Rightarrow\) góc BAD = góc BED
Mà góc BAD = 90 độ nên góc BED = 90 độ
\(\Rightarrow\)DE \(\perp\) BC
d)
Vì Δ ABD = Δ EBD (câu b)
\(\Rightarrow\) AD = ED
Xét Δ ADK và Δ EDC có:
góc DAK = góc DEC = 90 độ
AD = ED (cmt)
góc ADK = góc EDC (đ²)
\(\Rightarrow\) Δ ADK = Δ EDC (cgv - gn)
\(\Rightarrow\) DK = DC và AK = EC ( 2 cạnh tương ứng )
e)
Ta có:
BA = BE (gt)
AK = EC (câu d)
\(\Rightarrow\) BA + AK = BE + EC \(\Rightarrow\) BK = BC \(\Leftrightarrow\) Δ BKC cân tại B (định nghĩa)
Mà BD là phân giác góc CBK
\(\Rightarrow\) BD vừa là phân giác vừa là đường cao của Δ BKC
\(\Rightarrow\) BD ⊥ CK
#Tiểu Cừu
a) XÉT \(\Delta ABD\)VÀ \(\Delta EBD\)CÓ
BD LÀ CẠNH CHUNG
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
AB = BE (GT)
=> \(\Delta ABD\)=\(\Delta EBD\)(C-G-C)
C) VÌ \(\Delta ABD\)=\(\Delta EBD\)(CMT)
=> \(\widehat{BAD}=\widehat{BED}=90^o\)
=> DE VUÔNG GÓC VỚI BC (ĐPCM )
D) vì \(\Delta ABD\)=\(\Delta EBD\)(CMT )
=> AD = ED ( HAI CẠNH TƯƠNG ỨNG )
XÉT \(\Delta ADK\)VÀ \(\Delta EDC\)CÓ
\(\widehat{KAD}=\widehat{CED}=90^o\)
AD = ED (CMT)
\(\widehat{ADK}=\widehat{EDC}\left(Đ^2\right)\)
=> \(\Delta ADK\)=\(\Delta ADK\)(G-C-G)
=> DK = DC (ĐPCM)
=> AK = EC (ĐPCM)
e ) vì \(\Delta ABD\)=\(\Delta EBD\)(CMT)
=>\(\widehat{ADB}=\widehat{EDB}\)
TA CÓ
\(\widehat{ADB}=\widehat{D_1}\)(ĐỐI DỈNH)
\(\widehat{EDB}=\widehat{D_2}\)(ĐỐI ĐỈNH)
MÀ \(\widehat{ADB}=\widehat{EDB}\)
=> \(\widehat{D_1}=\widehat{D_2}\)
GỌI O LÀ GIAO ĐIỂM CỦA BD LÀ KC
XÉT \(\Delta KDO\)VÀ \(\Delta CDO\)CÓ
\(KD=CD\left(cmt\right)\)
\(\widehat{D_1}=\widehat{D_2}\)(CMT)
DO LÀ CẠNH CHUNG
=> \(\Delta KDO\)=\(\Delta CDO\)(C-G-C)
=> \(\widehat{KOD}=\widehat{COD}\)
MÀ HAI GÓC NÀY KỀ BÙ
\(\Rightarrow\widehat{KOD}=\widehat{COD}=\frac{180^o}{2}=90^o\)
\(\Rightarrow BD\perp CK\left(đpcm\right)\)

a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)

4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.

a, Số đo góc ABC la :
goc A+goc B+goc C=180
130+C=180
C=50
=> số đo góc ABD là : goc ABD=1/2gocC=>25
b, Xet 2 tam giac ABD va BDE
Co:AB=BE
goc ABD=goc DBE (250)
BD canh chung =>dpcm
mình biết làm mấy câu đầu rồi, mình chỉ bí câu cuối thôi
sai đề rồi bạn ơi
đúng r mà b