TV
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 6 2019
Xét \(\Delta HAC\)vuông tại H có HN là đường trung tuyến ứng với cạnh huyền
=> HN = NC = NA = AC/2
=> AC = 2HN = 8
Tương tự AB = 6
Theo hệ thức lượng trong tam giác vuông cho tam giác ABC vuông tại A có AH là đường cao thì
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{1}{6^2}+\frac{1}{8^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{25}{576}\)
\(\Leftrightarrow AH=\frac{24}{5}\)
Áp dụng định lí Pytago vào \(\Delta HAC\)vuông tại H có
\(HA^2+HC^2=AC^2\)
\(\Leftrightarrow\left(\frac{24}{5}\right)^2+HC^2=8^2\)
\(\Leftrightarrow HC=\frac{32}{5}\)
Tương tự \(HB=\frac{18}{5}\)
21 tháng 7 2023
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
HB=15^2/25=9cm
HC=25-9=16cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=25/7
=>BD=75/7cm; CD=100/7cm
b: ΔAHB vuông tại H có HI là đường cao
nên AI*AB=AH^2
ΔAHC vuông tại H có HK là đường cao
nên AK*AC=AH^2
=>AI*AB=AK*AC
c: AI*AB=AK*AC
=>AI/AC=AK/AB
=>ΔAIK đồng dạng với ΔACB
H
2
30 tháng 8 2018
Cho tam giác ABC vuông tại A, AH là đường cao. Biết AB=15cm,HC=16cm.Tính BC,AH,HB,AC.
24 tháng 8 2021
Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{7}\)
nên \(\dfrac{HB}{HC}=\dfrac{9}{49}\)
hay \(HB=\dfrac{9}{49}HC\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{9}{49}=42^2\)
hay HC=98cm
\(\Leftrightarrow HB=\dfrac{9}{49}\cdot98=18cm\)
24 tháng 8 2021
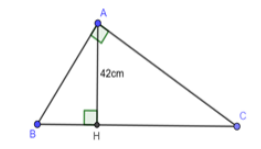
Ta có:\(\dfrac{AB}{AC}=\dfrac{3}{7}\) ⇒ AB = \(\dfrac{3}{7}\) AC
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{42^2}=\dfrac{49}{9AC^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{42^2}=\dfrac{49}{9AC^2}\)
⇔ \(AC^2=11368\Leftrightarrow AC=14\sqrt{58}\) \(\left(cm\right)\)
⇔ \(AB=\dfrac{3}{7}.14\sqrt{58}=6\sqrt{58}\) \(\left(cm\right)\)
Áp dụng định lý Pytago cho ABH vuông tại A có: \(AB^2+AC^2=BC^2\)
⇔ \(BC^2=\left(6\sqrt{58}\right)^2+\left(14\sqrt{58}\right)^2\)
⇔ \(BC^2=13456\Rightarrow BC=116\) \(cm\)
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
29 tháng 12 2019
Theo công hệ thức lương trong tam giác vuông ta có :
\(AB^2=BH.BC\Leftrightarrow9=1,8.BC\Rightarrow BC=5\left(cm\right)\)
Định lý Pytago :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
Như vậy khi ta quay tam giác ABC quanh trục AB ta thu được hình nón có đường cao \(AB=3\) , bán kính đáy \(AC=4\) và đường sinh \(BC=5\)
Diện tích xung quanh của hình nón thu được :
\(S_{xq}=\pi rl=\pi.AC.BC=20\pi\left(cm^2\right)\)
Thể tích hình nón là :
\(V=\frac{1}{3}\pi r^2h=\frac{1}{3}.\pi.4^2.3=16\pi\) ( cm khối )