Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: ΔABC vuông tại A
a) Xét ΔDAB vuông tại D và ΔACB vuông tại A có
\(\widehat{ABC}\) chung
Do đó: ΔDAB\(\sim\)ΔACB(g-g)
b) Xét ΔABC có
BE là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AE}{EC}=\dfrac{AB}{BC}\)(Định lí đường phân giác của tam giác)(1)
Ta có: ΔDAB\(\sim\)ΔACB(cmt)
nên \(\dfrac{AB}{BC}=\dfrac{BD}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)(2)
Từ (1) và (2) suy ra \(\dfrac{AE}{EC}=\dfrac{BD}{AB}\)
hay \(AE\cdot AB=BD\cdot EC\)(đpcm)

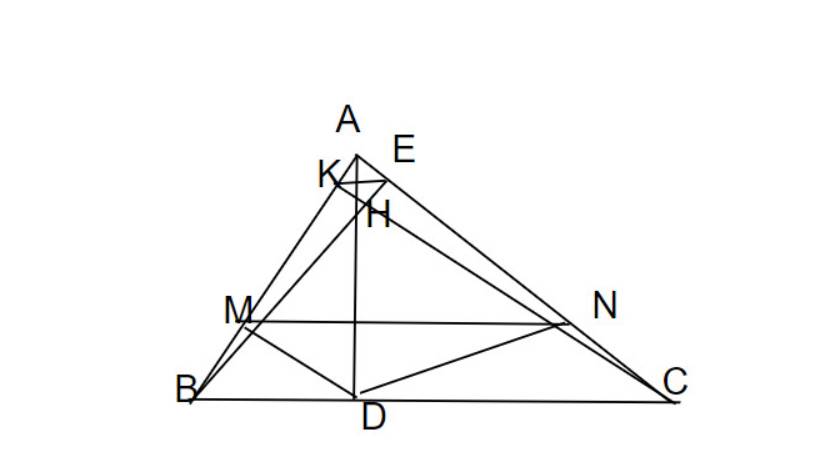
xét ΔAKH và Δ AMD, có
\(\widehat{A}=\widehat{A}\\ \widehat{K}=\widehat{M}=90^o\\ \Rightarrow\text{ }\Delta AKH\sim\Delta AMD\left(g-g\right)\)
\(\Leftrightarrow\dfrac{AH}{AD}=\dfrac{AK}{AM}\)(1)
xét ΔAKE và Δ AMN, có:
\(\widehat{A}\) chung
\(\widehat{E}=\widehat{N}\) đồng vị
\(\Rightarrow\text{ }\Delta AKE\sim\Delta AMN\left(g-g\right)\)
\(\Leftrightarrow\dfrac{AE}{AN}=\dfrac{AK}{AD}\)(2)
xét ΔAHE và Δ ADN, có:
\(\widehat{A}\) chung
từ (1) và (2) ta suy ra \(\dfrac{AH}{AD}=\dfrac{AE}{AN}\\ \Rightarrow\Delta AHE~\Delta ADN\)
\(\Leftrightarrow\widehat{E}=\widehat{N}=90^o\Rightarrow DN\perp AC\left(đpcm\right)\)
P/S: chúc bạn học tốt nhe, mình vẽ hình xong nhìn muốn nội thương=))

a, Xét ΔABC có góc BAC vuông
=> \(BC^2=AB^2+AC^2\)
=> \(BC^2=25\)
\(\Rightarrow BC=5\) (cm)
Xét ΔABC và ΔDAC, có
\(\widehat{BAC}=\widehat{ADC}\)
\(\widehat{C}\) chung
=> ΔABC∼ΔDAC(g.g)
=> \(\dfrac{AD}{AB}=\dfrac{AC}{BC}\)
=>\(\dfrac{AD}{3}=\dfrac{4}{5}\)
\(\Rightarrow AD=2,4cm\)
b, Vì ΔABC∼ΔDAC (cmt)
=>\(\dfrac{AC}{BA}=\dfrac{DC}{AC}\)
Xét ΔADB và ΔADC, có:
+ \(\widehat{ADC}=\widehat{ADB}\) (=90 độ)
+ \(\dfrac{AC}{BA}=\dfrac{DC}{AC}\)
=> ΔADB∼ΔADC (c.g.c)
=> \(\dfrac{AD}{BD}=\dfrac{DC}{AD}\)
\(\Rightarrow AD.AD=BD.DC\)
=> \(AD^2\)= BD.DC(đpcm)




a: Sửa đề: EA*EC=EB*EF
Xét ΔEAB và ΔEFC có
góc BEA=góc FEC
góc EFC=góc BAE
=>ΔEAB đồng dạng vơi ΔEFC
=>EA/EF=EB/EC
=>EA*EC=EB*EF
b: góc FCH=goc FBC=góc FBA
Xét ΔHCF và ΔFBC có
góc FCH=góc FBC
góc FHC=góc CFB=90 độ
=>ΔHCF đồng dạng vơi ΔFBC
=>góc BCF=góc HFC