Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo, có cả hình vẽ và bài làm nữa nhé: https://h7.net/hoi-dap/toan-7/chung-minh-tam-giac-bde-can-biet-cac-tam-giac-deu-abd-va-ace-faq380037.html

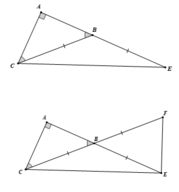
a) +) Chứng minh \(\Delta\)DAC = \(\Delta\)BAE
Thật vậy: Ta có: AD = AB ( \(\Delta\)DAB đều )
^DAB = ^CAE ( = 60\(^o\); \(\Delta\)DAB đều ; \(\Delta\)CAE đều ) => ^DAC = ^BAE
CA = AE ( \(\Delta\)CAE đều )
Từ 3 điều trên => \(\Delta\)DAC = \(\Delta\)BAE ( c.g.c) (1)
=> ^ABE = ^ADC (2)
+) Xét \(\Delta\)KAD và \(\Delta\)KIB có: ^DKA = ^BKI ( đối đỉnh )
^KDA = ^KBI( theo ( 2) )
mà ^DKA + ^KDA + ^KAD= ^BKI + ^KBI + ^KIB = 180\(^o\)
=> ^KIB = ^KAD = ^BAD= 60\(^o\)
=> ^DIB = 60\(^o\)
b) Từ (1) => DC = BE mà M là trung điểm DC; N là trung điểm BE
=> DM = BN (3)
+) Xét \(\Delta\)BAN và \(\Delta\)DAM
có: BN = DM ( theo (3)
^ABN = ^ADM ( theo (2)
AB = AD ( \(\Delta\)ADB đều )
=> \(\Delta\)BAN = \(\Delta\)DAM (4)
=> AN = AM => \(\Delta\)AMN cân tại A (5)
+) Từ (4) => ^BAN = ^DAM => ^BAM + ^MAN = ^DAB + ^BAM
=> ^MAN = ^DAB = 60\(^o\)(6)
Từ (5); (6) => \(\Delta\)AMN đều
c) +) Trên tia đối tia MI lấy điểm F sao cho FI = IB => \(\Delta\)FIB cân tại I
mà ^BIF = ^BID = 60\(^{\text{}o}\)( theo (a))
=> \(\Delta\)FIB đều (7)
=> ^DBA = ^FBI( =60\(^o\))
=> ^DBF + ^FBA = ^FBA + ^ABI
=> ^DBF = ^ABI
Lại có: BI = BF ( theo (7) ) và BA = BD ( \(\Delta\)BAD đều )
Từ (3) điều trên => \(\Delta\)DFB = \(\Delta\)AIB => ^AIB = ^DFB = 180\(\text{}^o\)- ^BFI = 180\(\text{}^o\)-60\(\text{}^o\)=120\(\text{}^o\)
+) Mặt khác ^BID = 60 \(\text{}^o\)( theo (a) )
=> ^DIE = 180\(\text{}^o\)- ^BID = 120 \(\text{}^o\)và ^DIA = ^AIB - ^BID = 120\(\text{}^o\)-60\(\text{}^o\)=60\(\text{}^o\)
=> ^AIE = ^DIE - ^DIA = 120\(\text{}^o\)-60\(\text{}^o\)=60\(\text{}^o\)
=> ^DIA = ^AIE ( = 60\(\text{}^o\))
=> IA là phân giác ^DIE.

Câu hỏi của Phạm Thùy Dung - Toán lớp 7 - Học toán với OnlineMath

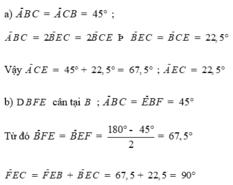
Tham khảo:
Chúc bạn học tốt!