Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





a) Chứng minh D E A ^ = 180 0
b) Chứng minh
A I M ^ = A K M ^ = I A K ^ = 90 0
c) Chứng minh DDME có E D M ^ = D E M ^ = 45 0
Þ DDME vuông cân ở M.
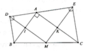

a: góc DAE=góc DAB+góc BAC+góc EAC
=45+90+45=180 độ
=>D,A,E thẳng hàng
b: ΔABC vuông tại A có AM là trung tuyến
nên MA=MB=MC
MA=MB
DA=DB
=>MD là trung trực của AB
=>MD vuông góc AB tại I
MA=MC
EA=EC
=>ME là trung trực của AC
=>ME vuông góc AC tại K
Xét tứ giác AIMK có
góc AIM=góc AKM=góc KAI=90 độ
=>AIMK là hình chữ nhật

Bài 1 :
a) Ta có : \(\hept{\begin{cases}AM=MB\\AN=NC\end{cases}\Rightarrow}\)MN là đường trung bình tam giác ABC \(\Rightarrow MN\text{//}BC\) hay \(MN\text{//}HK\left(1\right)\)
Dễ thấy MNKB là hình bình hành => \(\widehat{MNK}=\widehat{ABC}=\widehat{MHB}\)(Vì tam giác AHB vuông có HM là đường trung tuyến ứng với cạnh huyền.) . Mặt khác : \(\widehat{MNK}=\widehat{CKN}\)(hai góc ở vị trí so le trong)
=> \(\widehat{MHB}=\widehat{CKN}\). Mà hai góc này lần lượt bù với \(\widehat{MHK}\)và \(\widehat{HKN}\)=> \(\widehat{MHK}=\widehat{HKN}\) (2)
Từ (1) và (2) suy ra MNKH là hình thang cân.
b) Dễ thấy HK là đường trung bình tam giác AED => HK // ED hay BC // ED (3)
Tương tự , MH và NK lần lượt là các đường trung bình của các tam giác ABE và ACD
=> BE = 2MH ; CD = 2NK mà MH = NK (MNKH là hình thang cân - câu a)
=> BE = CD (4)
Từ (3) và (4) suy ra BCDE là hình thang cân.
Bài 2 :
a) Ta có : \(\widehat{BAD}=\widehat{CAE}=90^o\Rightarrow\widehat{BAD}+\widehat{DAE}=\widehat{CAE}+\widehat{DAE}\Rightarrow\widehat{BAE}=\widehat{CAD}\)
Xét tam giác BAE và tam giác CAD có : \(AB=AD\left(gt\right)\); \(AC=AE\left(gt\right)\) ; \(\widehat{BAE}=\widehat{CAD}\left(cmt\right)\)
\(\Rightarrow\Delta BAE=\Delta CAD\left(c.g.c\right)\Rightarrow CD=BE\)
b) Dễ dàng chứng minh được MP và PN lần lượt là các đường trung bình của các tam giác ACD và tam giác BEC
=> MP = 1/2CD ; PN = 1/2 BE mà CD = BE => MP = PN => tam giác MNP cân tại P
Để chứng minh góc MPN = 90 độ , hãy chứng minh BE vuông góc với CD.
bài khó quá ae júp cái =))
sorry anh em khong biet lam