Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAD vuông tai A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
Do đó: ΔBAD=ΔBHD
Suy ra: AD=HD
b: ta có: AD=HD
mà HD<DC
nen AD<DC
c: Xét ΔBHK vuông tại H và ΔBAC vuông tạiA có
BH=BA
góc HBK chung
Do đó:ΔBHK=ΔBAC
Suy ra BK=BC
hay ΔBKC cân tại B

a, Xét \(\Delta ABC\)VUÔNG tại A
Áp dụng định lý pitago ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB^2=BC^2-AC^2\)
\(\Rightarrow AB^2=10^2-6^2\)
\(\Rightarrow AB^2=100-36\)
\(\Rightarrow AB^2=64\)
\(\Rightarrow AB=\sqrt{64}=8\)
VẬY AB=8 cm
b, Xét \(\Delta ABD\)và \(\Delta HBD\)CÓ:
\(\widehat{BAD}=\widehat{BHD}=90độ\)
\(\widehat{ABD}=\widehat{HBD}\)(do BD là tia phân giác của \(\widehat{B}\))
BD là cạnh chung
\(\Rightarrow\Delta ABD=\Delta HBD\)(ch-gn)
\(\Rightarrow AD=HD\)(2 CẠNH TƯƠNG ỨNG)
c,Do \(\Delta ABD=\Delta HBD\left(câub\right)\)
\(\Rightarrow\widehat{BDA}=\widehat{BDH}\)(2 góc tương ứng)
lại có \(\widehat{ADK}=\widehat{HDC}\)(đối đỉnh)
\(\Rightarrow\widehat{BDA}+\widehat{ADK}=\widehat{BDH}+\widehat{HDC}\)
\(\Rightarrow\widehat{BDK}=\widehat{BDC}\)
Xét \(\Delta KBD\) VÀ \(\Delta CBD\)CÓ:
\(\widehat{ABD}=\widehat{CBD}\)(Do BD là tia phân giác của \(\widehat{B}\))
BD là cạnh chung
\(\widehat{BDK}=\widehat{BDC}\left(cmt\right)\)
Do đó \(\Delta KBD=\Delta CBD\left(g-c-g\right)\)
\(\Rightarrow BK=BC\)(2 CẠNH TƯƠNG ỨNG)
\(\Rightarrow\Delta KBC\) cân tại B

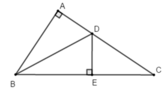
Từ D kẻ đường thẳng vuông góc với BC cắt BC tại E
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
BD cạnh huyền chung
A B D ^ = E B D ^ (BD là tia phân giác của góc B)
Khi đó: Δ A B D = Δ E B D (cạnh huyền góc nhọn)
Suy ra: AD = DE (hai cạnh tương ứng) (1)
Lại có tam giác DEC vuông tại E có DC là cạnh huyền
Suy ra DC > DE (trong tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất) (2)
Từ (1) và (2) suy ra DC > AD hay AD < DC
Vậy A đúng, B, C, D sai.
Chọn đáp án A

Kẻ DH ⊥ BC.
Xét hai tam giác vuông ABD và HBD, ta có:
∠B1 = ∠B2 ( vì BD là tia phân giác của góc ABC).
Cạnh huyền BD chung
∠BAD = ∠BHD = 90º
Suy ra: ΔABD = ΔHBD (cạnh huyền, góc nhọn)
⇒ AD = HD (2 cạnh tương ứng) (1)
Trong tam giác vuông DHC có ∠DHC = 90o
⇒ DH < DC (cạnh góc vuông nhỏ hơn cạnh huyền) (2)
Từ (1) và (2) suy ra: AD < DC

Câu B:
Xét hai tam giác vuông ABD và HBD, ta có:
∠B1 = ∠B2 ( vì BD là tia phân giác của góc ABC).
Cạnh huyền BD chung
∠BAD = ∠BHD = 90º
Suy ra: ΔABD = ΔHBD (cạnh huyền, góc nhọn)
⇒ AD = HD (2 cạnh tương ứng) (1)
Trong tam giác vuông DHC có ∠DHC = 90o
⇒ DH < DC (cạnh góc vuông nhỏ hơn cạnh huyền) (2)
Từ (1) và (2) suy ra: AD < DC

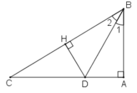
a)Có AB\(\perp\)AC;xy\(\perp\) AC
=>AB//xy
=> ABD=DEC(2 góc sole trong) (P/s: Góc nhé.)
Mà ABD=DBC(Vì BD-phân giác ABC)
=>DBC=DEC
=>Tam giác CBE cân
Vậy...
b) Có BDC là góc ngoài tại đỉnh D của tam giác ABD
=>BDC=ABD+BAD
=>BDC=ABD+90o
=>BDC là góc tù
Xét tam giác ABC có BAD=90o
=>BD lớn nhất(quan hệ góc-cạnh đối diện)=>BD>BA(1)
Xét tam giác BDC có BDC là góc tù
=>BC lớn nhất=>BC>BD(2)
Từ (1)(2)=>BC>BA
Mà BC=CE(Vì tam giác CBE cân)
=>CE>AB
Vậy...
c) Xét tam giác DCE có DCE=90o
=>DE lớn nhất(qh góc-cạnh đối diện)
=>DE>CE
Mà CE>BD(cmt)
=>DE>BD
Kẻ từ B đến AC có BD là đường xiên;AD là hình chiếu của BD
Kẻ từ E đến AC có DE là đường xiên;DC là hình chiếu của DE
Mà DE>BD(cmt)
=>DC>AD(qh đường xiên-hình chiếu)
Vậy...
_Học tốt_

AD>AB
Áp dụng bài hình chiếu của tam giác vuông ấy bạn,hình như thế