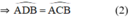Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc CIM=góc CNM=1/2*180=90 độ
=>NM vuông góc BC
góc MAB+góc MNB=180 độ
=>MABN nội tiếp
góc CAB=góc CIB=90 độ
=>CIAB nội tiếp
b: góc ANM=góc MBA
góc INM=góc ICA
mà góc MBA=góc ICA
nên góc ANM=góc INM
=>NM là phân giác của góc ANI
c: Xét ΔBNM vuông tại N và ΔBIC vuông tại I có
góc NBM chung
=>ΔBNM đồng dạng với ΔBIC
=>BN/BI=BM/BC
=>BN*BC=BI*BM
Xét ΔCNM vuông tại N và ΔCAB vuông tại A có
góc NCM chung
=>ΔCNM đồng dạng với ΔCAB
=>CN/CA=CM/CB
=>CN*CB=CA*CM
=>BM*BI+CM*CA=BC^2=AB^2+AC^2

a: Gọi O là trung điểm của MC
=>O là tâm đường tròn đường kính MC
Xét (O) có
ΔCNM nội tiếp
CM là đường kính
Do đó: ΔCNM vuông tại N
=>MN\(\perp\)NC tại N
=>MN\(\perp\)CB tại N
Xét tứ giác ABNM có \(\widehat{MNB}+\widehat{MAB}=90^0+90^0=180^0\)
nên ABNM là tứ giác nội tiếp
=>A,B,N,M cùng thuộc một đường tròn
b: ABNM là tứ giác nội tiếp
=>\(\widehat{ANM}=\widehat{ABM}\)
=>\(\widehat{ANM}=\widehat{ABI}\)(1)
Xét tứ giác CIAB có \(\widehat{CIB}=\widehat{CAB}=90^0\)
nên CIAB là tứ giác nội tiếp
=>\(\widehat{ABI}=\widehat{ACI}\)
mà \(\widehat{ACI}=\widehat{MCI}=\widehat{MNI}\left(=\dfrac{1}{2}sđ\stackrel\frown{MI}\right)\)
nên \(\widehat{ABI}=\widehat{MNI}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{MNI}=\widehat{MNA}\)
=>NM là phân giác của góc ANI

Lời giải:
a) $\widehat{MNC}=90^0$ (góc nt chắn nửa đường tròn)
$\Rightarrow \widehat{BNM}=90^0$
$\Rightarrow \widehat{BNM}+\widehat{BAM}=90^0+90^0=180^0$
Tứ giác $ABNM$ có tổng 2 góc đối bằng $180^0$ nên là tgnt (đpcm)
$MNCI$ nội tiếp thì hiển nhiên rồi.
b) $\widehat{MIC}=90^0$ (góc nt chắn nửa đường tròn)
Vì $MNCI, ABNM$ nội tiếp nên:
$\widehat{MNI}=\widehat{MCI}=90^0-\widehat{IMC}=90^0-\widehat{BMA}=\widehat{ABM}=\widehat{ANM}$
Do đó $NM$ là tia phân giác $\widehat{ANI}$
c) Đề sai (nhìn hình)

Lời giải:
1.
$\widehat{MDC}=90^0$ (góc nt chắn nửa đường tròn)
$\Leftrightarrow \widehat{BDC}=90^0$
Tứ giác $ABCD$ có $\widehat{BAC}=\widehat{BDC}=90^0$ và cùng nhìn cạnh $BC$ nên là tgnt.
Do $ABCD$ nội tiếp nên $\widehat{BCA}=\widehat{BDA}$
Mà $\widehat{BDA}=\widehat{MCS}$ (do $MDSC$ nội tiếp)
$\Rightarrow \widehat{BCA}=\widehat{MCS}$
$\Rightarrow CA$ là phân giác $\widehat{BCS}$
2.
Gọi $T$ là giao điểm của $BA$ và $EM$
Xét tam giác $BTC$ có $TE\perp BC$ (do $\widehat{MEC}=90^0$) và $CA\perp BT$ và $TE, CA$ giao nhau tại $M$ nên $M$ là trực tâm tam giác $BTC$
$\Rightarrow BM\perp TC$.
Mà $BM\perp DC$ nên $TC\parallel DC$ hay $T,D,C$ thẳng hàng
Do đó $BA, EM, DC$ đồng quy tại $T$
3.
Vì $ABCD$ nt nên $\widehat{MAD}=\widehat{CAD}=\widehat{DBC}=\widehat{MBE}$
Dễ cm $BAME$ nội tiếp cho $\widehat{A}+\widehat{E}=90^0+90^0=180^0$ nên $\widehat{MBE}=\widehat{EAM}$
Do đó: $\widehat{MAD}=\widehat{EAM}$ nên $AM$ là tia phân giác $\widehat{EAM}(*)$
Mặt khác:
Cũng do $MECD,ABCD$ nội tiếp nên:
$\widehat{ADM}=\widehat{ADB}=\widehat{ACB}=\widehat{MCE}=\widehat{MDE}$
$\Rightarrow DM$ là tia phân giác $\widehat{ADE}(**)$
Từ $(*); (**)\Rightarrow M$ là tâm đường tròn nội tiếp $ADE$.

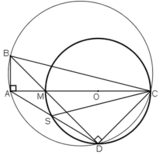
a) 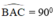 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
D ∈ đường tròn đường kính MC

⇒ D ∈ đường tròn đường kính BC
⇒ A, B, C, D cùng thuộc đường tròn đường kính BC
hay tứ giác ABCD nội tiếp.
b) Xét đường tròn đường kính BC:
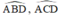 đều là góc nội tiếp chắn cung
đều là góc nội tiếp chắn cung 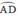
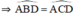
c) + Trong đường tròn đường kính MC:
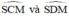 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 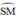
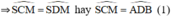
+ Trong đường tròn đường kính BC:
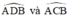 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung