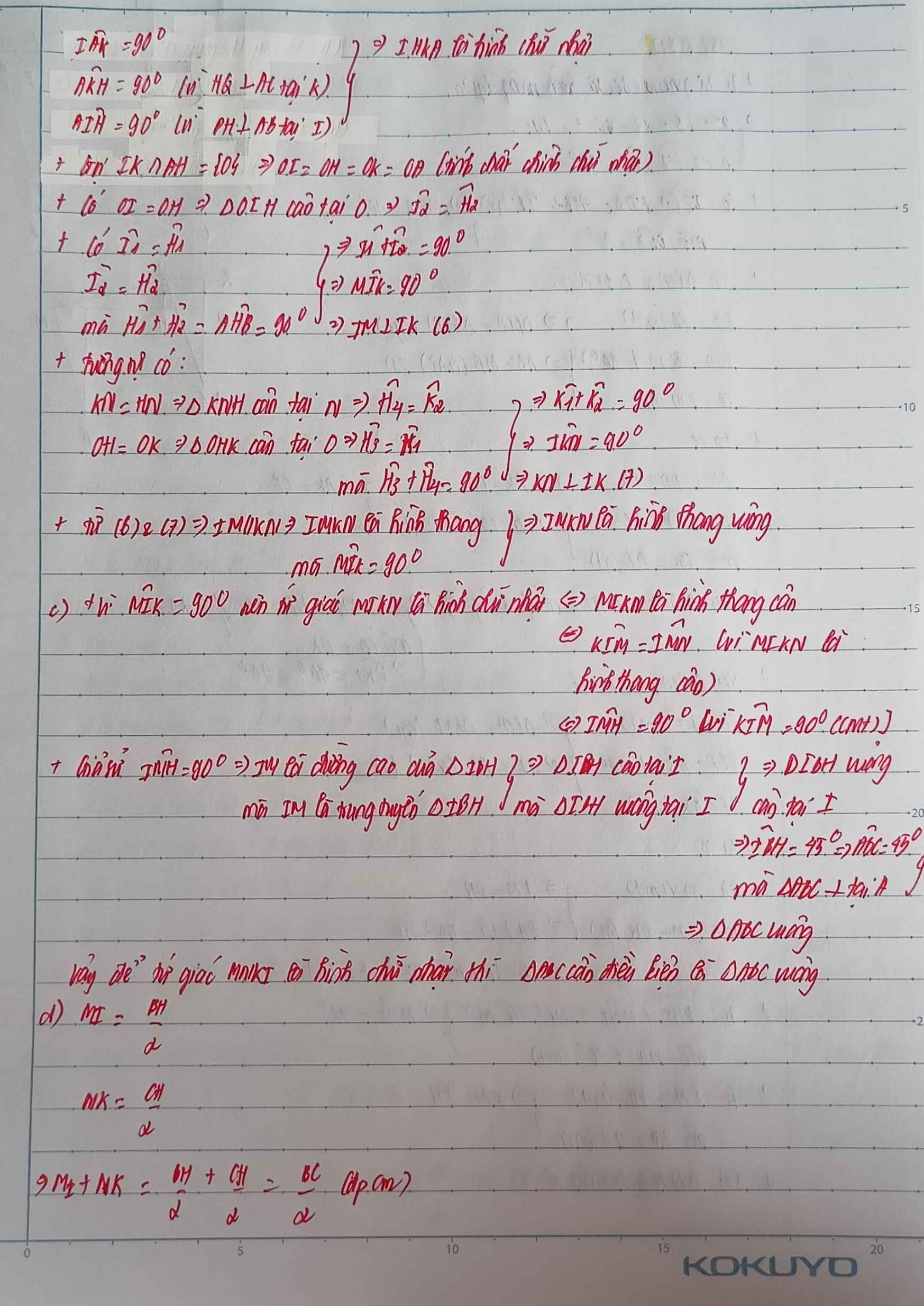Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AIMK có
\(\widehat{AIM}=\widehat{AKM}=\widehat{KAI}=90^0\)
Do đó: AIMK là hình chữ nhật

a: Xét tứ giác AIMK có
\(\widehat{AIM}=\widehat{AKM}=\widehat{KAI}=90^0\)
Do đó: AIMK là hình chữ nhật

a: Xét tứ giác AIMK có
\(\widehat{AIM}=\widehat{AKM}=\widehat{KAI}=90^0\)
Do đó: AIMK là hình chữ nhật

a) Xét tứ giác ABEC có
M là trung điểm của đường chéo BC(gt)
M là trung điểm của đường chéo AE(A và E đối xứng nhau qua M)
Do đó: ABEC là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành ABEC có \(\widehat{CAB}=90^0\)(ΔABC vuông tại A)
nên ABEC là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Vì D đối xứng với M qua AB(gt)
nên AB là đường trung trực của DM
⇔AB vuông góc với DM tại trung điểm của DM
mà AB cắt DM tại H(gt)
nên H là trung điểm của DM và MH⊥AB tại H
Ta có: MH⊥AB(cmt)
AC⊥AB(ΔABC vuông tại A)
Do đó: MH//AC(Định lí 1 từ vuông góc tới song song)
hay MD//AC
Ta có: H là trung điểm của MD(cmt)
nên \(MH=\dfrac{1}{2}\cdot MD\)(1)
Xét ΔABC có
M là trung điểm của BC(gt)
MH//AC(cmt)
Do đó: H là trung điểm của AB(Định lí 1 đường trung bình của tam giác)
Xét ΔABC có
M là trung điểm của BC(gt)
H là trung điểm của AB(cmt)
Do đó: MH là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒\(MH=\dfrac{1}{2}\cdot AC\)(Định lí 2 đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra AC=MD
Xét tứ giác ACMD có
AC//MD(cmt)
AC=MD(cmt)
Do đó: ACMD là hình bình hành(Dấu hiệu nhận biết hình bình hành)