Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tg ABD =tg EBD ( cm trên) •> AD=DE( 2 cạnh tương ứng) (1)
Tg ADF vg tại A=> Góc A lớn nhất=> FD lớn nhất( Qh giữa góc và cạnh đối diện trong 1 tam giác)=> AD<FD(2)
Từ 1 và 2 => ED<FD
a) Tam giác ABC vuông tại A => AB2+AC2=BC2 ( theo định lý Pitago)
=> 62+Ac2=102 =>AC2=100-36=64=> AC= 8
Vì D nằm trên AC=> AD+DC= AC=> 3+DC=8=> DC=5(cm)

a)Xét\(\Delta DEF\)có:\(EF^2=DE^2+DF^2\)(Định lý Py-ta-go)
hay\(5^2=3^2+DF^2\)
\(\Rightarrow DF^2=5^2-3^2=25-9=16\)
\(\Rightarrow DF=\sqrt{16}=4\left(cm\right)\)
Ta có:\(DE=3cm\)
\(DF=4cm\)
\(EF=5cm\)
\(\Rightarrow DE< DF< EF\)hay\(3< 4< 5\)
b)Xét\(\Delta DEF\)và\(\Delta DKF\)có:
\(DE=DK\)(\(D\)là trung điểm của\(EK\))
\(\widehat{EDF}=\widehat{KDF}\left(=90^o\right)\)
\(DF\)là cạnh chung
Do đó:\(\Delta DEF=\Delta DKF\)(c-g-c)
\(\Rightarrow EF=KF\)(2 cạnh t/ứ)
Xét\(\Delta KEF\)có:\(EF=KF\left(cmt\right)\)
Do đó:\(\Delta KEF\)cân tại\(F\)(Định nghĩa\(\Delta\)cân)
c)Ta có:\(DF\)cắt\(EK\)tại\(D\)là trung điểm của\(EK\Rightarrow DF\)là đg trung tuyến xuất phát từ đỉnh\(F\)của\(\Delta KEF\)
\(KI\)cắt\(EF\)tại\(I\)là trung điểm của\(EF\Rightarrow KI\)là đg trung tuyến xuất phát từ đỉnh\(K\)của\(\Delta KEF\)
Ta lại có:\(DF\)cắt\(KI\)tại\(G\)
mà\(DF\)là đg trung tuyến xuất phát từ đỉnh\(F\)của\(\Delta KEF\)
\(KI\)là đg trung tuyến xuất phát từ đỉnh\(K\)của\(\Delta KEF\)
\(\Rightarrow G\)là trọng tâm của\(\Delta KEF\)
\(\Rightarrow GF=\frac{2}{3}DF\)(Định lí về TC của 3 đg trung tuyến của 1\(\Delta\))
\(=\frac{2}{3}.4=\frac{8}{3}\approx2,7\left(cm\right)\)
Vậy\(GF\approx2,7cm\)

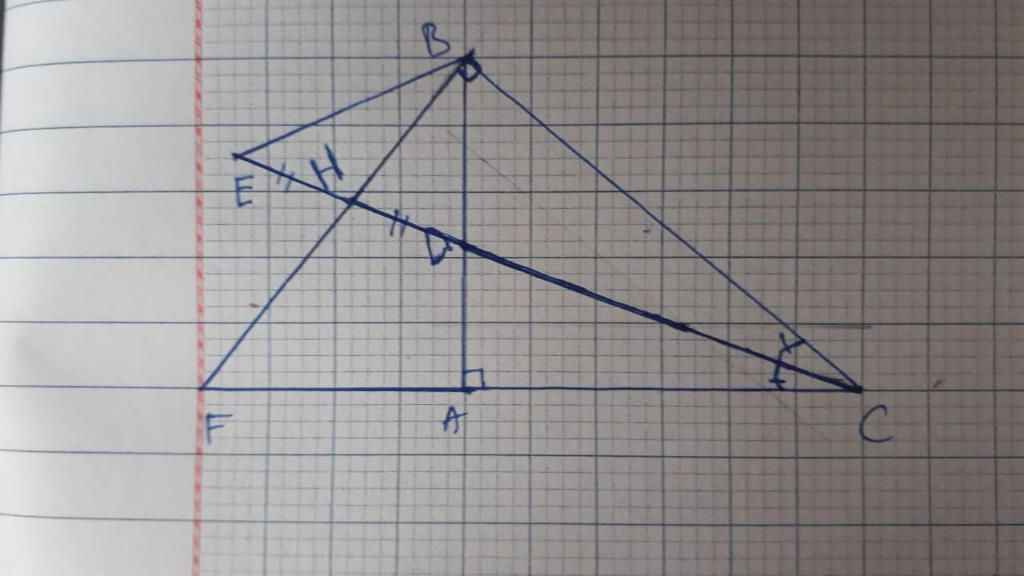
a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE