Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMBE có
D là trung điểm của AB
D là trung điểm của ME
Do đó: AMBE là hình bình hành
mà MA=MB
nên AMBE là hình thoi

a: Xét tứ giác AEBM có
D la trung điểm chung của AB và EM
MA=MB
Do đó: AEBM là hình thoi
b: Xét tứ giác AEMC có
AE//MC
AE=MC
Do đó: AEMC là hình bình hành
=>AM cắt EC tại trung điểm của mỗi đường
=>E,I,C thẳng hàng
c: Để AEBM là hình vuông thì góc AMB=90 độ
=>AM vuông góc với BC
=>ΔABC cân tại A

a: Xét tứ giác AEBM co
D là trung điểm chung của AB và ME
MA=MB
DO đó: AEBM là hình thoi
b: Xét tứ giác AEMC có
AE//MC
AE=MC
Do đó: AEMC là hình bình hành
=>AM cắt EC tại trung điểm của mỗi đường
=>E,I,C thẳng hàng
c: Để AEBM là hình vuông thì góc AMB=90 độ
=>AM vuông góc với BC
=>ΔABC cân tại A
=>AB=AC

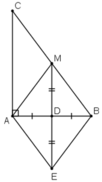
a) Ta có MB = MC, DB = DA
⇒ MD là đường trung bình của ΔABC
⇒ MD // AC
Mà AC ⊥ AB
⇒ MD ⊥ AB.
Mà D là trung điểm ME
⇒ AB là đường trung trực của ME
⇒ E đối xứng với M qua AB.
b) + MD là đường trung bình của ΔABC
⇒ AC = 2MD.
E đối xứng với M qua D
⇒ D là trung điểm EM
⇒ EM = 2.MD
⇒ AC = EM.
Lại có AC // EM
⇒ Tứ giác AEMC là hình bình hành.
+ Tứ giác AEBM là hình bình hành vì có các đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành AEBM lại có AB ⊥ EM nên là hình thoi.
c) Ta có: BC = 4cm ⇒ BM = 2cm
Chu vi hình thoi AEBM bằng 4.BM = 4.2 = 8cm
d)- Cách 1:
Hình thoi AEBM là hình vuông ⇔ AB = EM ⇔ AB = AC
Vậy nếu ABC vuông có thêm điều kiện AB = AC (tức tam giác ABC vuông cân tại A) thì AEBM là hình vuông.
- Cách 2:
Hình thoi AEBM là hình vuông ⇔ AM ⊥ BM
⇔ ΔABC có trung tuyến AM là đường cao
⇔ ΔABC cân tại A.
Vậy nếu ΔABC vuông có thêm điều kiện cân tại A thì AEBM là hình vuông.

a. Xét tứ giác AEBM có:
+ D là trung điểm AB (gt).
+ D là trung điểm EM (E là điểm đối xứng với M qua D).
\(\Rightarrow\) Tứ giác AEBM là hình bình hành (dhnb).
Mà AB \(\perp\) EM (E là điểm đối xứng với M qua D).
\(\Rightarrow\) Tứ giác AEBM là hình thoi (dhnb).
b. Tứ giác AEBM là hình thoi (cmt).
\(\Rightarrow\) AE = BM; AE // BM (tính chất hình thoi).
Ta có: M là trung điểm BC (AM là đường trung tuyến tam giác ABC).
\(\Rightarrow\) BM = CM.
Mà AE = BM (cmt).
\(\Rightarrow\) AE = CM.
Xét tứ giác AEMC có:
+ AE = CM (cmt).
+ AE // CM (AE // BM).
\(\Rightarrow\) Tứ giác AEMC là hình bình hành (dhnb).
c. Tứ giác AEBM là hình vuông (giả thiết).
\(\Rightarrow\) AM \(\perp\) BM (tính chất hình vuông).
\(\Rightarrow\) AM \(\perp\) BC.
Xét tam giác ABC vuông tại A có:
+ AM là đường trung tuyến tam giác ABC (gt).
Mà AM là đường cao (AM \(\perp\) BC).
\(\Rightarrow\) Tam giác ABC vuông cân tại A.
Vậy tam giác ABC vuông cân tại A thì AEBM là hình vuông.