Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
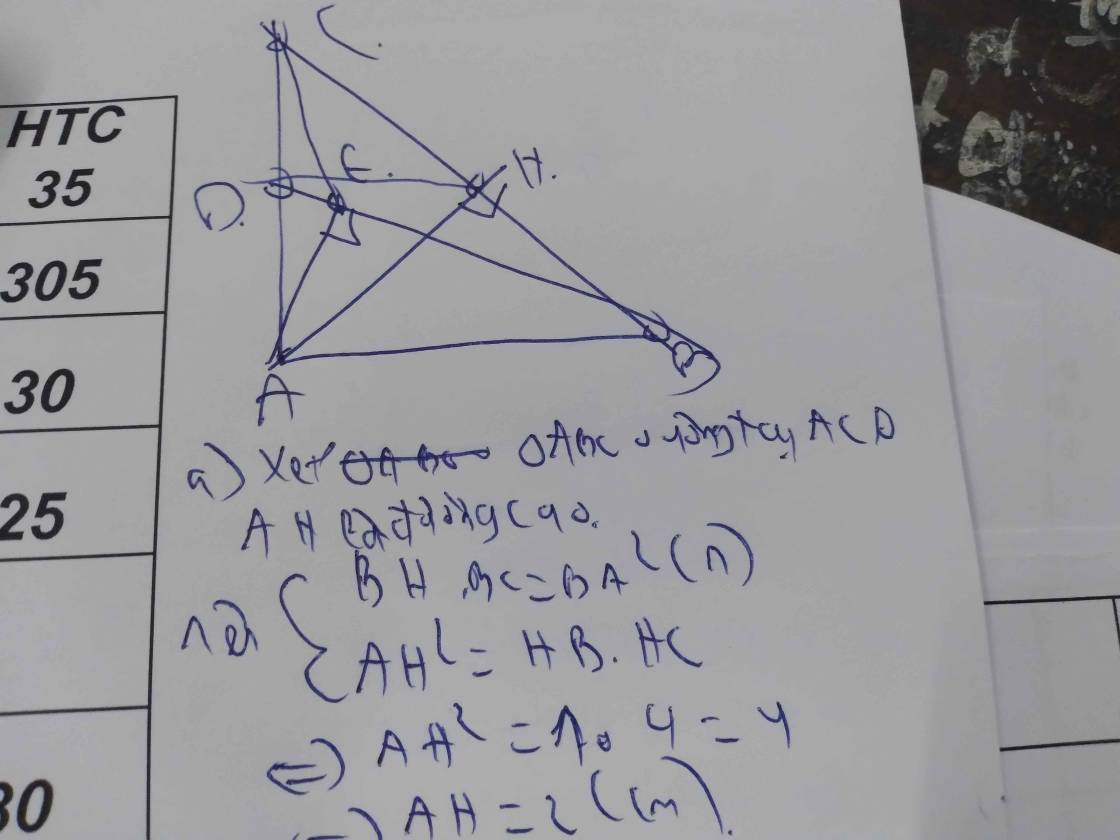
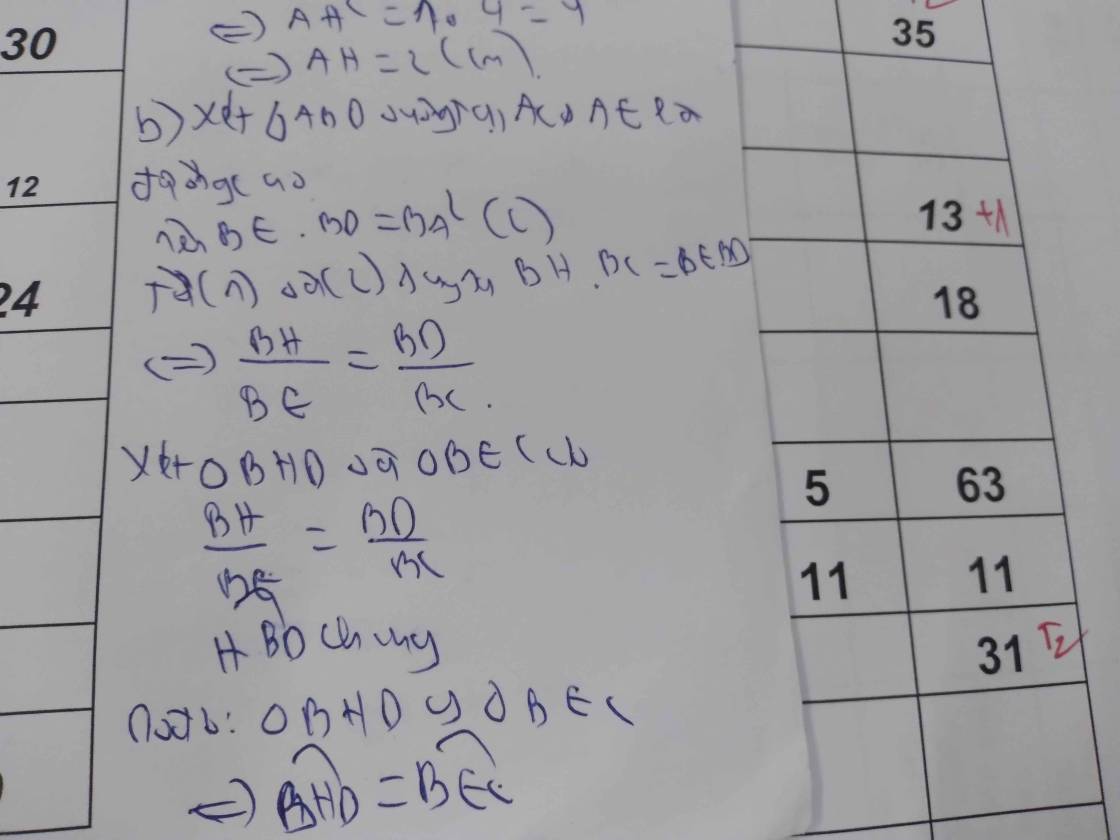
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
b: Xét ΔABD có
AH vừa là đường cao, vừa là trung tuyến
=>ΔABD cân tại A
=>tan ADH=tan ABD=tan ABC=AC/AB=4/3
Xét ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC=HD*HC
Câu 1:
a: Xét ΔAHB vuông tạiH có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
b: \(BC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
\(AH=\dfrac{4\cdot6}{2\sqrt{13}}=\dfrac{12}{\sqrt{13}}\left(cm\right)\)
\(AE=\dfrac{AH^2}{AC}=\dfrac{144}{13}:6=\dfrac{24}{13}\left(cm\right)\)
1 phần thôi nhé
Nối BE, Gọi P là giao điểm của AD với BE.
Áp dụng định lí Ceva cho tam giác ABE => AH/HE=BP/PE=> HP//AB(1).
Từ (1)=> Tam giác AHP cân tại H=> AH=HP.(2)
Ta cần chứng minh AD//CE <=> DP//CE <=> BD/BC=BP/BE <=> BD/BC=1-(EP/BE).(3)
Mà EP/BE=HP/AB (do (1))=> EP/BE= AH/AB=HD/DB (do (2) và tc phân giác). (4)
Khi đó (3)<=> BD/BC=1-(HD/DB) hay (BD/BC)+(HD/DB)=1 <=> BD^2+HD*BC=BC*DB
<=> BD^2+HD*BC= (BD+DC)*BD <=> BD^2+HD*BC= BD^2+BD*DC <=> HD*BC=BD*DC
<=> HD/DB=CD/BC <=> AH/AB=CD/BC. (5)
Chú ý: Ta cm được: CA=CD (biến đổi góc).
Nên (5) <=> AH/AB=CA/BC <=> Tg AHB đồng dạng Tg CAB.( luôn đúng)
=> DpCm.
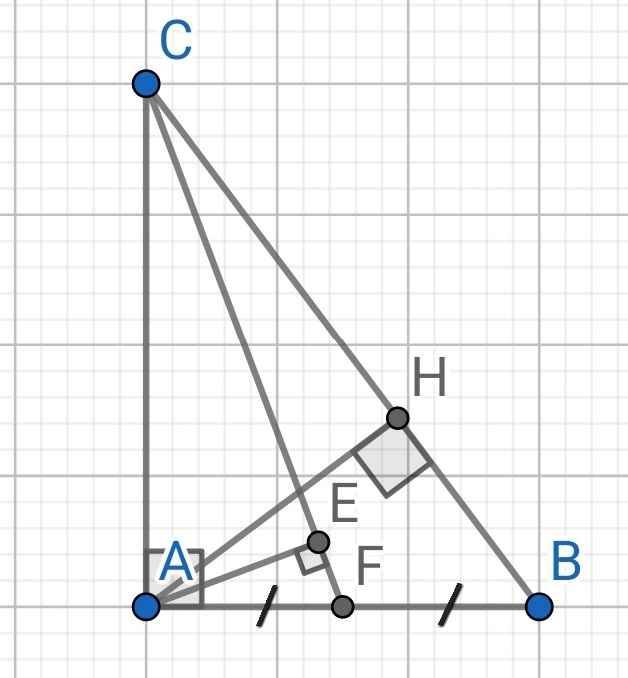a) ∆ABC vuông tại A có AH là đường cao
⇒ AH² = BH . CH
= 9 . 16
= 144
⇒ AH = 12 (cm)
BC = BH + CH
= 9 + 16
= 25 (cm)
∆ABC vuông tại A có AH là đường cao
⇒ AB² = BH . BC
= 9 . 25
= 225
⇒ AB = 15 (cm)
AC² = CH . BC
= 16 . 25
= 400
⇒ AC = 20 (cm)
b) Do F là trung điểm AB
⇒ AF = AB : 2 = 15 : 2 = 7,5 (cm)
∆ACF vuông tại A
⇒ tanAFC = AC/AF = 20/7,5 = 8,3
⇒ ∠AFC ≈ 69⁰
c) Do AE ⊥ CF (gt)
⇒ AE là đường cao của ∆ACF
∆ACF vuông tại C có CE là đường cao
⇒ AC² = CE.CF (1)
∆ABC vuông tại A có AH là đường cao
⇒ AC² = BC.CH (2)
Từ (1) và (2) suy ra:
CE.CF = BC.CH
d) Ta có: \(\angle HDA=\angle HEA=\angle DAE=90\Rightarrow HDAE\) là hình chữ nhật
\(\Rightarrow DE=AH=\sqrt{BH.HC}=\sqrt{4.9}=6\left(cm\right)\)
Ta có: \(DM\parallel EN (\bot DE)\) và \(\angle MDE=\angle DEN=90\)
\(\Rightarrow MDEN\) là hình thang vuông
Vì \(\Delta BDH\) vuông tại D có M là trung điểm BH
\(\Rightarrow MD=\dfrac{1}{2}BH=\dfrac{1}{2}.4=2\left(cm\right)\)
Vì \(\Delta HEC\) vuông tại E có M là trung điểm CH
\(\Rightarrow EN=\dfrac{1}{2}CH=\dfrac{1}{2}.9=\dfrac{9}{2}\left(cm\right)\)
\(\Rightarrow S_{DENM}=\dfrac{1}{2}.\left(DM+EN\right).DE=\dfrac{1}{2}.\left(2+\dfrac{9}{2}\right).6=\dfrac{39}{2}\left(cm^2\right)\)
a: BC=BH+CH
=2+8
=10(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{2\cdot8}=4\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{2\cdot10}=2\sqrt{5}\left(cm\right)\\AC=\sqrt{8\cdot10}=4\sqrt{5}\left(cm\right)\end{matrix}\right.\)
b: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
=>DE=AH
c: ΔHDB vuông tại D
mà DM là đường trung tuyến
nên DM=HM=MB
\(\widehat{EDM}=\widehat{EDH}+\widehat{MDH}\)
\(=\widehat{EAH}+\widehat{MHD}\)
\(=90^0-\widehat{C}+\widehat{C}=90^0\)
=>DE vuông góc DM
