Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lý Pitago cho tam giác vuông ACH:
\(AC=\sqrt{AH^2+HC^2}=10\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông ABC:
\(AC^2=CH.BC\Rightarrow BC=\dfrac{AC^2}{CH}=\dfrac{25}{2}\) (cm)
\(\Rightarrow BH=BC-CH=\dfrac{9}{2}\left(cm\right)\)
Pitago tam giác vuông ABC:
\(AB=\sqrt{BC^2-AC^2}=\dfrac{15}{2}\left(cm\right)\)
b.
Áp dụng hệ thức lượng cho tam giác vuông ACH:
\(HD.AC=AH.HC\Rightarrow HD=\dfrac{AH.HC}{AC}=\dfrac{24}{5}\left(cm\right)\)
Tiếp tục là hệ thức lượng:
\(AH^2=AD.AC\Rightarrow AD=\dfrac{AH^2}{AC}=\dfrac{18}{5}\left(cm\right)\)
\(S_{AHD}=\dfrac{1}{2}AD.HD=\dfrac{216}{25}\left(cm^2\right)\)

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
b: Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
c:
Sửa đề: AP là phân giác của góc BAC
Xét tứ giác AEPF có
\(\widehat{AEP}=\widehat{AFP}=\widehat{FAE}=90^0\)
=>AEPF là hình chữ nhật
Hình chữ nhật AEPF có AP là phân giác của góc FAE
nên AEPF là hình vuông

a: BC=căn 6^2+8^2=10cm
AH=6*8/10=4,8cm
c:
Xét tứ giác ANHM có
góc ANH=góc AMH=góc MAN=90 độ
=>ANHM là hình chữ nhật
AD vuông góc MN
=>góc DAC+góc ANM=90 độ
=>góc DAC+góc AHM=90 độ
=>góc DAC+góc ABC=90 độ
=>góc DAC=góc DCA
=>DA=DC
góc DAC+góc DAB=90 độ
góc DCA+góc DBA=90 độ
mà góc DAC=góc DCA
nên góc DAB=góc DBA
=>DA=DB
=>DB=DC
=>D là trung điểm của BC

\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=10^2-6^2=64\)
=>\(AC=\sqrt{64}=8\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}\simeq53^0\)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\)
=>\(BH\cdot10=6^2=36\)
=>BH=36/10=3,6(cm)
ΔAHB vuông tại H
=>\(S_{HAB}=\dfrac{1}{2}\cdot HA\cdot HB=\dfrac{1}{2}\cdot4,8\cdot3,6=8,64\left(cm^2\right)\)
a) Để tính độ dài đường cao \(AH\) và số đo \(\angle B\), chúng ta có thể sử dụng các quy tắc trong tam giác vuông.
Chúng ta biết rằng trong tam giác vuông, độ dài của đường cao \(AH\) từ đỉnh vuông \(A\) xuống cạnh huyền \(BC\) có thể được tính bằng công thức:
\[AH = \frac{1}{2} \times BC\]
Trong trường hợp này:
\[AH = \frac{1}{2} \times 10 \, \text{cm} = 5 \, \text{cm}\]
Số đo của góc \(\angle B\) có thể được tính bằng cách sử dụng hàm tan trong tam giác vuông:
\[\tan B = \frac{AH}{AB}\]
\[\angle B = \arctan\left(\frac{AH}{AB}\right)\]
Trong trường hợp này:
\[\tan B = \frac{5}{6}\]
\[\angle B = \arctan\left(\frac{5}{6}\right)\]
Bạn có thể sử dụng máy tính để tính toán giá trị chính xác của \(\angle B\).
b) Để tính diện tích tam giác \(AHB\), chúng ta sử dụng công thức diện tích tam giác:
\[S_{AHB} = \frac{1}{2} \times \text{độ dài } AH \times \text{độ dài } AB\]
Trong trường hợp này:
\[S_{AHB} = \frac{1}{2} \times 5 \, \text{cm} \times 6 \, \text{cm} = 15 \, \text{cm}^2\]
Vậy, độ dài của đường cao \(AH\) là \(5 \, \text{cm}\), số đo của góc \(\angle B\) có thể được tính, và diện tích tam giác \(AHB\) là \(15 \, \text{cm}^2\).
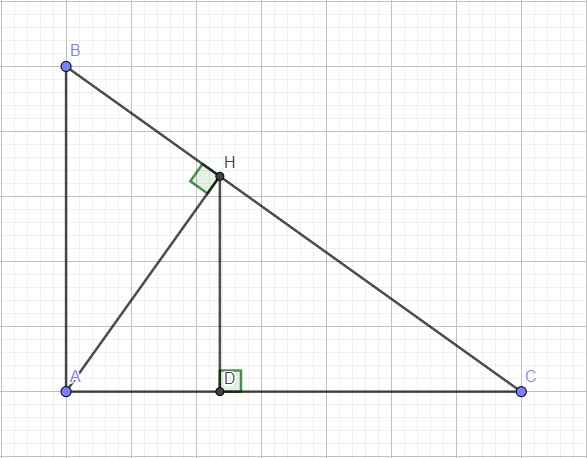
a: BC=10cm
AH=4,8cm
BH=3,6cm
b: Xét ΔABC vuông tại A có
\(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{C}=53^0\)
a: BC=10cm
AH=4,8cm
BH=3,6cm
b: Xét ΔABC vuông tại A có
sinB=ACBC=45sinB=ACBC=45
nên ˆC=530