Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.Xét \(\Delta ADB\)và \(\Delta CAB\)có:
\(\widehat{ADB}=\widehat{CAB}=90^o\)
\(\widehat{ABC}\)chung
\(\Rightarrow\Delta ADB~\Delta CAB\left(g.g\right)\)
b.Kí hiệu: \(\widehat{ABE}=\widehat{B_1};\widehat{EBC}=\widehat{B_2}\)
Ta có:\(\widehat{B}=2\widehat{C}\)
\(\Rightarrow\widehat{B_1}=\widehat{B_2}=\widehat{C}\)
Vì \(\Delta ADB~\Delta CAB\left(g.g\right)\)
\(\Rightarrow\frac{AB}{AE}=\frac{AC}{AB}\)
\(\Rightarrow AB^2=AE.AC\)
c.Ta có:\(\Delta ABB~\Delta CAB\left(g.g\right)\)(cm câu a)
\(\Rightarrow\frac{BA}{BC}=\frac{BD}{AB}\)
Theo t/c đường p/g ta có: \(\frac{BA}{BC}=\frac{EA}{EC}\)và \(\frac{BD}{BA}=\frac{FD}{FA}\)
\(\Rightarrow\frac{FD}{FA}=\frac{EA}{EC}\left(đpcm\right)\)
d.Ta có:\(AB=2BD\left(gt\right)\)
\(\Rightarrow\frac{BD}{AB}=\frac{1}{2}\)
Mà \(\frac{BD}{AB}=\frac{FD}{FA}\)(câu c)
\(\Rightarrow\frac{BD}{AB}=\frac{FD}{FA}=\frac{1}{2}\)
\(\Rightarrow FA=2FD\)
Mà \(S_{ABC}=\frac{1}{2}BC.AD\)
và \(S_{BFC}=\frac{1}{2}BC.FD\)
\(\Rightarrow S_{ABC}=3S_{BFC}\left(đpcm\right)\)


a) ΔADB và ΔABC vuông có ∠B chung ∠ ΔADB ∼ ΔCAB (g.g)
b) Vì ∠B = 2∠C (gt) ∠ ∠B1 = ∠B2 = ∠C
Do đó hai tam giác vuông ABE và ACB đồng dạng (g.g)
![]()
c) Ta có ΔADB ∼ ΔCAB (cmt)
![]()
Theo tính chất đường phân giác ta có :

d) Ta có AB = 2BD (gt)
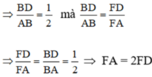
![]()


Tk mình đi mọi người mình bị âm nè!
Ai tk mình mình tk lại cho

a) Xét tam giác ADB và tam giác BAC, ta có:
Góc B chung
Góc D = góc A (=900)
=> Tam giác ADB đồng dạng tam giác CAB
b) Ko biết chứng minh cái gì
c) Có tam giác ADB đồng dạng tam giác CAB (cmt)
\(\Rightarrow\frac{BD}{AB}=\frac{AB}{BC}\left(1\right)\)
Xét tam giác ABD, có BF là tia phân giác
\(\Rightarrow\frac{AF}{AB}=\frac{FD}{BD}\Rightarrow\frac{BD}{AB}=\frac{DF}{FA}\left(2\right)\)
Xét tam giác ABD, có BD là tia phân giác
\(\Rightarrow\frac{AE}{AB}=\frac{EC}{BC}\Rightarrow\frac{AB}{AE}=\frac{BC}{EC}\Rightarrow\frac{AB}{BC}=\frac{AE}{EC}\left(3\right)\)
Từ (1); (2) và (3)
\(\Rightarrow\frac{DF}{FA}=\frac{AE}{EC}\)

a: Xét ΔADB vuông tại D và ΔCAB vuông tại A có
góc B chung
=>ΔADB đồng dạng với ΔCAB
b: Xét ΔABE vuông tại A và ΔACB vuông tại A có
góc ABE=góc ACB
=>ΔABE đồng dạng với ΔACB
=>AB/AC=AE/AB
=>AB^2=AC*AE
c: DF/FA=DB/AB
AE/EC=BA/BC
mà DB/AB=BA/BC
nên DF/FA=AE/EC