Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xet ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE và DA=DE
=>BD là trung trựccủa AE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=gócEDC
=>ΔDAF=ΔDEC
=>DF=DC
c: AD=DE
mà DE<DC
nên AD<DC
d: Xet ΔBFC có BA/AF=BE/EC
nên AE//CF

Xét tam giác ABD và tam giác EBD có:
Góc ABD=Góc EBD(doBD là phân giác góc B)
góc BAD=góc EAD(=90 độ)
BD chung
suy ra tam giác ABD =tam giác EBD(cạnh huyền góc nhọn)
suy ra AB=EB suy ra B nằm trên đường trung trực AE(1)
vì tam giác ABD =tam giác EBD suy ra ED=AD suy raD thuộc đường trung trực AE(2)
Từ 1 và 2 suy ra BD thuộc đường trung trực AE
b)Xét tam giácADF và tam giác EDC có:
AD=ED
góc ADF=góc EDC
gócA =góc E=90 độ
Suy ra tam giác ADF =tam giác EDC(g.c.g)
suy ra DF=DC
c)tam giác DEC có :DE<DC
mà DA=DE
suy raDA<DC
d)Vì AB=BE và AF=EC suy ra BF=BC suy ra B thuộc đường trung trực FC(1)
Lại có :DF=DC suy ra D thuộc đường trung trựcFC(2)
Từ 1 và 2 suy raBD thuộc đường trung trực FC
suy raBD vuông góc với FC
Mà BD vuông góc với AE
suy ra AE//FC

a:Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE và DA=DE
=>BD là trung trực của AE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=góc EDC
=>ΔDAF=ΔDEC
=>DF=DC
c: AD=DE
DE<DC
=>AD<DC

a, Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E ta có:
BD:cạnh chung; góc ABD= góc EBD(gt)
Do đó tam giác ABD=tam giác EBD(cạnh huyền - góc nhọn)
=> AB=EB; AD=ED(cặp cạnh tương ứng)
Vì AB=EB; AD=ED nên B là D nằm trên đường trung trực của AE
=> BD là đường trung trực của AE(đpcm)
b, Xét tam giác ADF và tam giác EDC ta có:
góc FAD=góc CED(=90độ);AD=ED(cmt); góc ADF=góc EDC(đối đỉnh)
Do đó tam giác ADF=tam giác EDC(g.c.g)
=> DF=DC(cặp cạnh tương ứng) (đpcm)
c, Xét tam giác DEC vuông tại E ta có:
DE<DC(do trong tam giác vuông cạnh huyền lớn nhất)
mà DE=DA=> DA<DC(đpcm)
d, Vì tam giác ADF=tam giác EDC(cm câu b)
=> AF=EC(cặp cạnh tương ứng)
Ta có: BF=BA+AF; BC=BE+EC
mà BA=BE;AF=EC(đã cm)
=> BF=BC
=> tam giác BCF cân tại B
mặc khác ta có: BA=BE(cm câu a)
=> tam giác ABE cân tại B
Xét tam giác BCF và tam giác ABE cân tại B ta có:
góc BAE=\(\dfrac{180^o-\text{góc}ABE}{2}\) ;góc BFC=\(\dfrac{180^o-\text{góc}FBC}{2}\)
=> góc BAE=góc BFC
=> AE//CF(do có 1 cặp góc bằng nhau ở vị trí đồng vị) (đpcm)

10 năm sau thì cha vẫn hơn con 24 tuổi
Ta có sơ đồ 10 năm sau :
Cha : |----|----|----|
Con : |----|
Tuổi con 10 năm sau là :
24: ( 3- 1 ) = 12 ( tuổi )
Tuổi con hiện nay là :
12 - 10 = 2 tuổi
Tuổi cha hiện nay là :
2 + 24 =26 ( tuổi )
Đáp số : .......
Sau 10 năm cha vẫn hơn con 24 tuổi.
=>Tuổi con 10 năm sau là: 24:(3-1)=12(tuổi)
Tuổi con hiện nay là: 12-10=2(tuổi)
Tuổi cha hiện nay là: 2+24=26(tuổi)
Đ/s:...
Bài này dễ như ăn cháo.

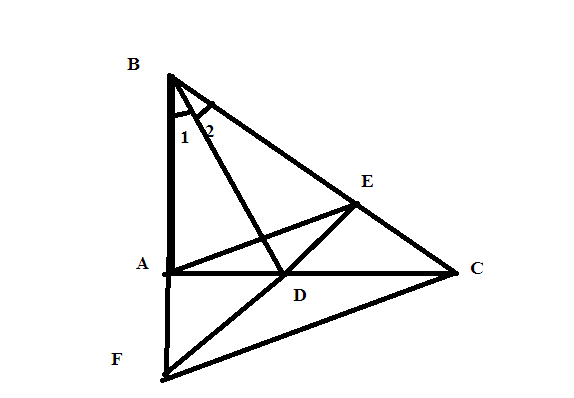
Xét ΔBAD và ΔBDE có:
BD là cạnh chung
B1=B2 (BD là tia phân giác của \(\widehat{B}\))
BA = BE (GT)
Nên ΔBAD= ΔBDE (c.g.c)
=>\(\widehat{ADB}=\widehat{BDE}\)
Ta có:\(\widehat{ADB}+\widehat{ADF}=\widehat{BDF}\)
\(\widehat{BDE}+\widehat{EDC}=\widehat{BDC}\)
Mà :\(\widehat{ADB}=\widehat{BDE}\)(CMT)
\(\widehat{ADF}=\widehat{EDC}\)( 2 góc đối đỉnh)
=>\(\widehat{BDF}=\widehat{BDC}\)
Xét ΔBDF và Δ BDC, có:
\(\widehat{BDF}=\widehat{BDC}\)
BD là cạnh chung
B1=B2
Nên ΔBDF=ΔBDC (g.c.g)
=>DC = DF
b)Ta có:ΔEDC vuông tại E=> DC là cạnh lớn nhất hay DC>DE
MÀ DE=AD (ΔBAD và ΔBDE)
=> AD< DC
c) Ta có BE=BA=>ΔBEA cân tại B
Mà BD là tia phân giác=>BD là đường trung trực
Vì :ΔBDF=ΔBDC=>BF=BC
=>ΔBFC cân tại B=>\(\widehat{C}=\widehat{F}\)
Ta có:\(\widehat{B}+\widehat{C}+\widehat{F}=180^o\)
=>\(\widehat{B}+\widehat{C}.2=180^O\)
=>\(\widehat{C}=\dfrac{180^O-\widehat{B}}{2}\)(1)
vÌ ΔBAE cân tại B
Tương tự ta có:
\(\widehat{E}=\dfrac{180^o-\widehat{B}}{2}\)(2)
Từ (1) và (2)=> \(\widehat{E}=\widehat{C}\)
Mà 2 góc này ở vị trí đồng vị=>AE // FC

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: BA=BE
DA=DE
=>BD là trung trực của AE
c: Xét ΔBFC có
FE,CA là đường cao
FE cắt CA tại D
=>D là trực tâm
=>BD vuông góc FC


Xét tam giác ABD và tam giác EBD có:
Góc ABD=Góc EBD(doBD là phân giác góc B)
góc BAD=góc EAD(=90 độ)
BD chung
suy ra tam giác ABD =tam giác EBD(cạnh huyền góc nhọn)
suy ra AB=EB suy ra B nằm trên đường trung trực AE(1)
vì tam giác ABD =tam giác EBD suy ra ED=AD suy raD thuộc đường trung trực AE(2)
Từ 1 và 2 suy ra BD thuộc đường trung trực AE
b)Xét tam giácADF và tam giác EDC có:
AD=ED
góc ADF=góc EDC
gócA =góc E=90 độ
Suy ra tam giác ADF =tam giác EDC(g.c.g)
suy ra DF=DC
c)tam giác DEC có :DE<DC
mà DA=DE
suy raDA<DC
d)Vì AB=BE và AF=EC suy ra BF=BC suy ra B thuộc đường trung trực FC(1)
Lại có :DF=DC suy ra D thuộc đường trung trựcFC(2)
Từ 1 và 2 suy raBD thuộc đường trung trực FC
suy raBD vuông góc với FC
Mà BD vuông góc với AE
suy ra AE//FC
ai mk lại
Xét tam giác ABD và tam giác EBD có:
Góc ABD=Góc EBD(doBD là phân giác góc B)
góc BAD=góc EAD(=90 độ)
BD chung
suy ra tam giác ABD =tam giác EBD(cạnh huyền góc nhọn)
suy ra AB=EB suy ra B nằm trên đường trung trực AE(1)
vì tam giác ABD =tam giác EBD suy ra ED=AD suy raD thuộc đường trung trực AE(2)
Từ 1 và 2 suy ra BD thuộc đường trung trực AE
b)Xét tam giácADF và tam giác EDC có:
AD=ED
góc ADF=góc EDC
gócA =góc E=90 độ
Suy ra tam giác ADF =tam giác EDC(g.c.g)
suy ra DF=DC
c)tam giác DEC có :DE<DC
mà DA=DE
suy raDA<DC
d)Vì AB=BE và AF=EC suy ra BF=BC suy ra B thuộc đường trung trực FC(1)
Lại có :DF=DC suy ra D thuộc đường trung trựcFC(2)
Từ 1 và 2 suy raBD thuộc đường trung trực FC
suy raBD vuông góc với FC
Mà BD vuông góc với AE
suy ra AE//FC