
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=50^2-30^2=1600\)
=>AC=40(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=HB\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(BH=\dfrac{30^2}{50}=18\left(cm\right);CH=\dfrac{40^2}{50}=32\left(cm\right)\)
Áp dụng định lý Pytago vào \(\Delta ABC\) vuông tại A ta có:
\(AB^2+AC^2=BC^2\Rightarrow AC^2=BC^2-AB^2=50^2-30^2=1600\Rightarrow AC=\sqrt{1600}=40\left(cm\right)\)
Áp dụng định lý Pytago vào \(\Delta ABH\) vuông tại H ta có: \(AH^2+BH^2=AB^2\Rightarrow24^2+BH^2=30^2\Rightarrow BH^2=30^2-24^2=324\Rightarrow BH=\sqrt{324}=18\left(cm\right)\)\(HC=BC-BH=50-18=32\left(cm\right)\)

Bài 3 :
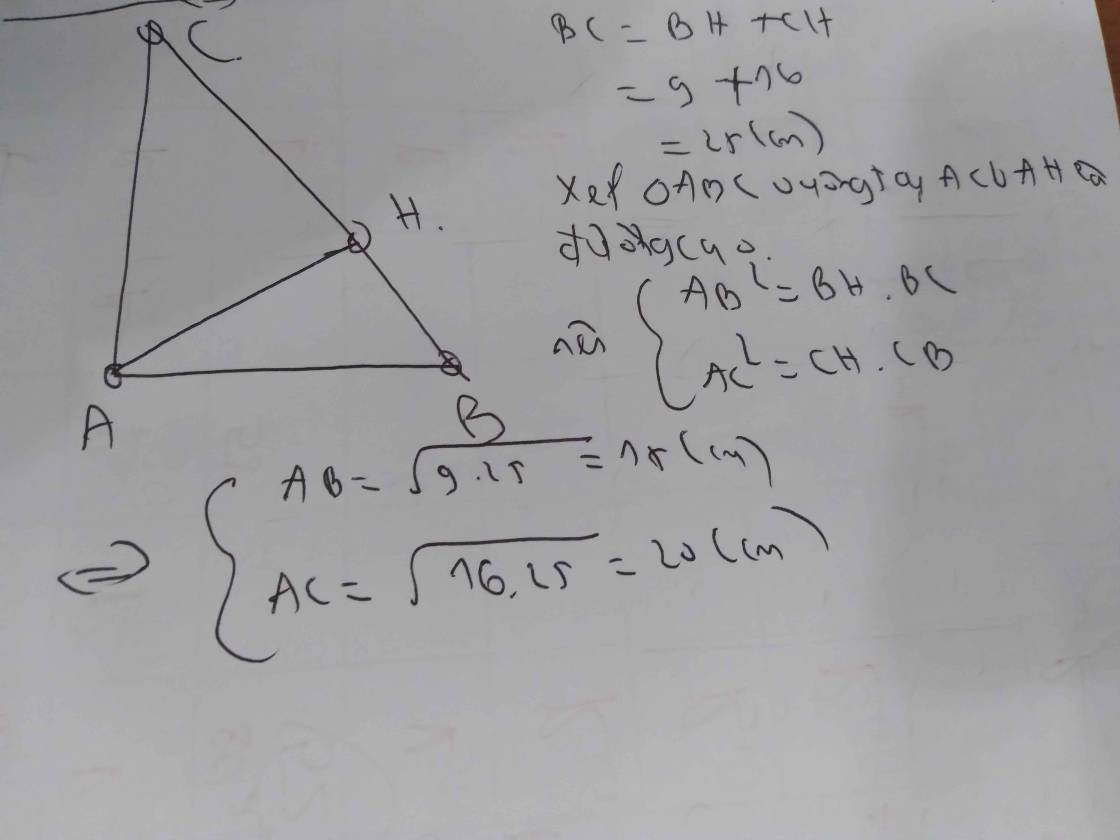
\(BC=HC+HB=16+9=25\left(cm\right)\)
\(BC^2=AB^2+AC^2\Rightarrow AB^2=BC^2-AC^2=25^2-20^2=625-400=225=15^2\)
\(\Rightarrow AB=15\left(cm\right)\)
\(AH^2=HC.HB=16.9=4^2.3^2\Rightarrow AH=3.4=12\left(cm\right)\)
Bài 6:
\(AB=AC=4\left(cm\right)\) (Δ ABC cân tại A)
\(BH=HC=2\left(cm\right)\) (Ah là đường cao, đường trung tuyến cân Δ ABC)
\(BC=BH+HC=2+2=4\left(cm\right)\)
Chu vi Δ ABC :
\(4+4+4=12\left(cm\right)\)

a, Xét tam giác HBA và tam giác ABC có
^B _ chung ; ^BHA = ^BAC = 900
Vậy tam giác HBA ~ tam giác ABC (g.g)
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=10cm\)
\(\dfrac{AH}{AC}=\dfrac{AB}{BC}\Rightarrow AH=\dfrac{48}{10}=\dfrac{24}{5}cm\)
\(\dfrac{BH}{AB}=\dfrac{AB}{BC}\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{36}{10}=\dfrac{18}{5}cm\)
b, Xét tam giác CHI và tan giác CAH có
^AIH = ^CHA = 900
^C _ chung
Vậy tam giác CHI ~ tam giác CAH (g.g)
\(\dfrac{CH}{AC}=\dfrac{CI}{CH}\Rightarrow CH^2=CI.AC\)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{H}\) chung
Do đó: ΔHBA\(\sim\)ΔABC
b: Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=225\)
hay BC=15cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH=\dfrac{12\cdot9}{15}=7.2\left(cm\right)\)

a) xét tam giác ABC và HAC có:
góc CAB=gócCHA=90độ
chung ACH
suy ra tam giác ABCđồng dạng với tam giác HAC
=> \(\frac{BC}{AC}=\frac{AC}{CH}=>AC^2=BC\cdot CH\)
b) vì tam giác ABC vuông tại A,áp dụng định lý pitago bạn sẽ tính được BC
thay vào \(\frac{BC}{AC}=\frac{AC}{CH}\)
bạn sẽ tính được CH,sau đó tương tự áp dụng pitago cho các tam giác còn lai là ra nhé
kết quả:HC=9,6;AH=7,2;BH=5,4

a, Xét tứ giác ABKC có: AC // BK ( cùng vuông góc vs AB)
=> Tứ giác ABKC là hình thang
mà \(\widehat{A}=90^o\)=> Tứ giác ABKC là hình thang vuông
b) Ta có: AC // BK => \(\widehat{AKB}=\widehat{CAH}\)( 2 góc so le trong)
Xét tam giác ABK và tam giác CHA có:
\(\widehat{ABK}=\widehat{CHA}\left(=90^o\right)\)
\(\widehat{AKB}=\widehat{CAH}\)(cmt)
=> Tam giác ABK đồng dạng với tam giác CHA
=> \(\frac{AB}{AK}=\frac{CH}{AC}\)=> AB. AC = AK.CH (đpcm)
c) Xét tam giác ABH và tam giác CAH có:
\(\widehat{AHB}=\widehat{CHA}\left(=90^o\right)\)
\(\widehat{BAH}=\widehat{ACH}\)( cùng phụ với góc HAC)
=> Tam giác ABH đồng dạng với tam giác CAH
=> \(\frac{AH}{BH}=\frac{CH}{AH}\)=> \(AH^2=BH.CH\)
d) Ta có: \(AH^2=BH.CH\)(cmc) => \(AH=\sqrt{BH.CH}=\sqrt{9.16}=12\)(cm)
Xét tam giác ABH vuông tại H, ta có: \(AB^2=BH^2+AH^2\)(định lý Pytago)
=> \(AB=\sqrt{BH^2+AH^2}=\sqrt{9^2+12^2}=15\)(cm)
Vậy AB = 15cm, AH = 12cm
Chúc bạn học tốt