Question

[Tram phan]

cho tam giác ABC vuông tại A có AB=AC trên BC lấy diểm E hạ BH và CK cùng vuông góc với tai AE.C/M BH=Ak

Answer 1

[Phan Văn Toàn]

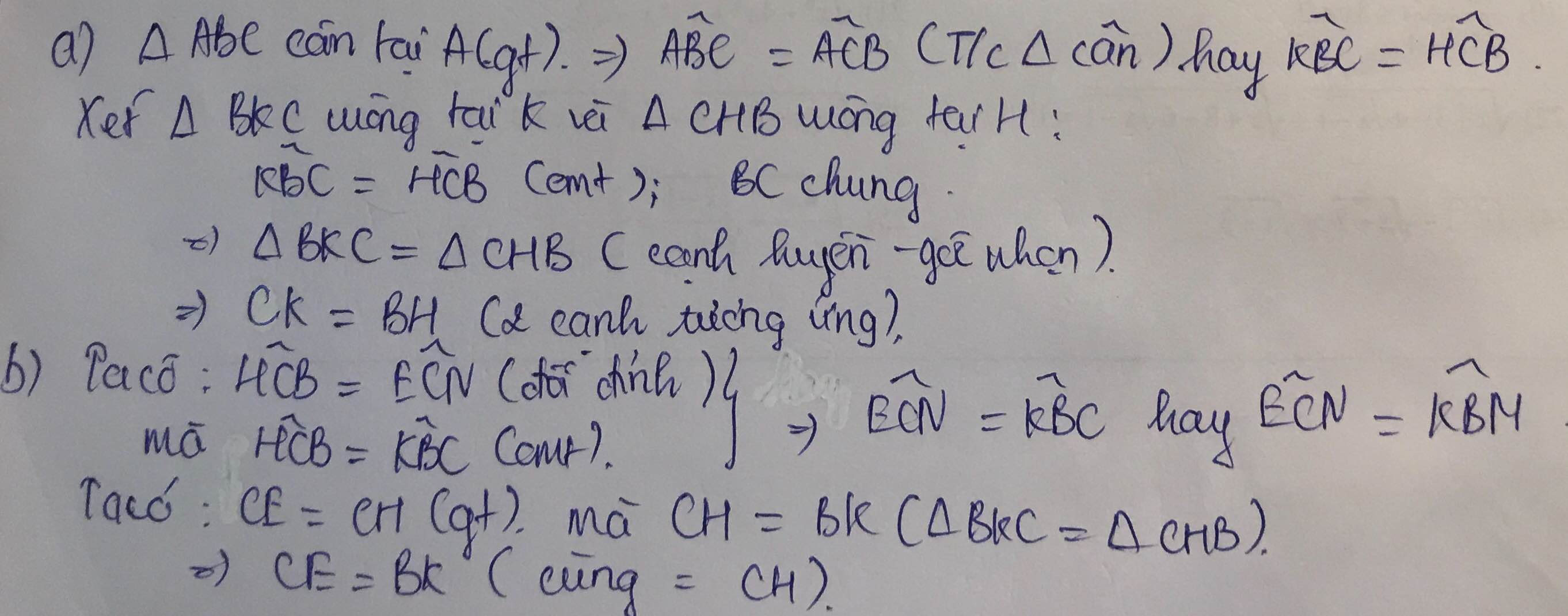
Để chứng minh BH/AK = CM, ta sẽ sử dụng định lí đồng dạng tam giác. Gọi M là trung điểm của BC. Ta có AB = AC và BM = MC (do M là trung điểm của BC), nên tam giác ABC là tam giác đều. Khi đó, ta có: - Tam giác ABH và tam giác AKM là đồng dạng (cùng có góc vuông tại H và K, cùng có góc A). - Tam giác ACM và tam giác ABM là đồng dạng (cùng có góc vuông tại M, cùng có góc A). Từ đó, ta có tỉ số đồng dạng: BH/AK = AB/AM (từ tam giác ABH và tam giác AKM) = AC/AM (vì AB = AC) = CM/BM (từ tam giác ACM và tam giác ABM) = CM/CK (vì BM = CK) Vậy, ta có BH/AK = CM/CK.

Answer 2

[Akai Haruma]

Lời giải:

Xét tam giác $BAH$ và $ACK$ có:

$BA=AC$

$\widehat{BHA}=\widehat{AKC}=90^0$

$\widehat{BAH}=\widehat{ACK}$ (cùng phụ $\widehat{KAC}$)

$\Rightarrow \triangle BAH=\triangle ACK$ (ch-gn)

$\Rightarrow BH=AK$