Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

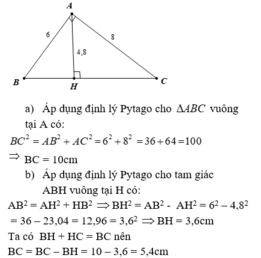
a. Áp dụng định lí Pytago trong tam giác ABC ta có:
BC2 = AB2 + AC2 = 62 + 82 = 100 ⇒ BC = 10cm

a.Tam giác ABC vuông tại A \(\Rightarrow AB^2+AC^2=BC^2\)\(\Rightarrow5^2+12^2=BC^2\Rightarrow169=BC^2\Rightarrow BC=13\left(cm\right)\)
b. Tam giác MNP là tam giác vuông vì \(6^2+8^2=10^2\)
Chúc bạn học tốt!

a: BC=căn 6^2+8^2=10cm
AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔBAK vuông tại A và ΔBHK vuông tại H có
BK chung
góc ABK=góc HBK
=>ΔBAK=ΔBHK
c: Xét ΔKAI vuông tại A và ΔKHC vuông tại H có
KA=KH
AI=HC
=>ΔKAI=ΔKHC
=>góc AKI=góc HKC
=>góc AKI+góc AKH=180 độ
=>I,K,H thẳng hàng
d: Xét ΔBIC có BA/AI=BH/HC
nên AH//IC

a: BC=căn 6^2+8^2=10cm
b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
c Xét ΔBHF vuông tại H và ΔBAC vuông tại A có
BH=BA
góc HBF chung
=>ΔBHF=ΔBAC
=>BF=BC
mà góc FBC=60 độ
nên ΔBFC đều

Tự vẽ hình nha !!!
a) Áp dụng định lý Py-ta-go ta có
AB2 + AC2 = BC2
=> 82 + 62 = BC2
=> BC = 10 cm
b) Ta có BA = AD
=> AC là trung tuyến của BD
Vì \(AC\Omega BK=\left\{E\right\}\)
=> E là trọng tâm của tam giác BDC
=> \(\frac{EC}{AC}=\frac{2}{3};\frac{AE}{AC}=\frac{1}{3}\)mà AC = 6 cm
=> EC = 4 cm ; AE = 2 cm
c) Xét tam giác BAC và tam giác DAC có
\(\hept{\begin{cases}BA=AD\\\widehat{CAB}=\widehat{CAD=90^{\text{o}}}\\AC\text{ chung}\end{cases}}\Rightarrow\Delta BAC=\Delta DAC\left(c.g.c\right)\)
=> BC = DC (cạnh tương ứng)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
b) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)(AD là tia phân giác của \(\widehat{HAK}\))
Do đó: ΔAHD=ΔAKD(cạnh huyền-góc nhọn)
c) Ta có: ΔADH vuông tại H(gt)
nên \(\widehat{HDA}+\widehat{HAD}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{BDA}+\widehat{HAD}=90^0\)(2)
Ta có: \(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}\)(tia AD nằm giữa hai tia AB,AC)
nên \(\widehat{BAD}+\widehat{KAD}=90^0\)(3)
Từ (2) và (3) suy ra \(\widehat{BDA}=\widehat{BAD}\)
Xét ΔBAD có \(\widehat{BDA}=\widehat{BAD}\)(cmt)
nên ΔBAD cân tại B(Định lí đảo của tam giác cân)

Ban xem o dinh li pita go phan hinh hoc ay BC= 10 CM TICK NHE
tích đi giải cho