Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trên tia đối AB lấy I sao cho AI = AB
- Vẽ hình chữ nhật AINC ( IN // AC ; IN = AC )
Do AB = 1/3 AC => AD = AB => AD=AI . Lấy M thuộc IN sao cho IM = AD
Ta có hình vuông IAMD => IA = IM = MD = DA
Xét MBI và
CMN
MI=NC (và IANC là hình chữ nhật)
BI=MN ( vì và IA = IM \Rightarrow
)
(gt)
\Leftrightarrow MBI =
CMI (c - g - c)
\Rightarrow ; BM = CM \Rightarrow
BMC cân ở M (|-)1)
Xét BIM và
EAB
AB = MI
AE = BI
\Leftrightarrow BIM =
EAB (c - g - c)
\Rightarrow (góc tương ứng)
Ta có:
Mà:
\Rightarrow
\Rightarrow BMC vuông ở M
![]() -*2)
-*2)
Từ (|-)1) và ![]() -*2)
-*2)
\Rightarrow MCB vuông cân ở M
\Rightarrow hay
Lại có:
\Rightarrow (đpcm)
:-*:-*:-*:-*:-*|-)|-)|-):-SS:-SS![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Cách 1:
Kẻ DM ∟ AC sao cho DM = AB.
Dễ dàng chứng minh Δ DMC = Δ AEB (c - g - c)
=> ^DCM = ^AEB và BE = MC (1)
Δ BMD = Δ BED (c - g - c)
=> ^BMD = ^BED và BM = BE (2)
(1) và (2) cho:
^DCM = ^BMD và CM = MB
=> Δ BMC cân tại M
mà ^DMC + ^DCM = 90o (Δ MDC vuông)
=> ^DMC + ^BMD = 90o
=> Δ BMC vuông cân.
=> BCM = 45o
Mà ^ACB + ^DCM = ^BCM
=> ^ACB + ^AEB = 45o (vì ^AEB = ^DCM (cmt))
Cách 2:
Đặt AB = a
ta có: BD = a√2
Do DE/DB = DB/DC = 1/√2
=> Δ DBC đồng dạng Δ DEB (c - g - c)
=> ^DBC = ^DEB
Δ BDC có ^ADB góc ngoài
=> ^ADB = ^DCB + ^DBC
hay ^ACB + ^AEB = 45o
Cách 3
ta có:
tanAEB = AB/AE = 1/2
tanACB = AB/AC = 1/3
tan (AEB + ACB) = (tanAEB + tanACB)/(1 - tanAEB.tanACB)
= (1/2 + 1/3)/(1 - 1/2.1/3) = 1 = tan45o
Vậy ^ACB + ^AEB = 45o.

a: \(\dfrac{DE}{DB}=\dfrac{a}{a\sqrt{2}}\)
\(\dfrac{DB}{DC}=\dfrac{a}{a\sqrt{2}}\)
Do đó: DE/DB=DB/DC
b: Xét ΔBDE và ΔCDB có
DB/DC=DE/DB
góc BDE=góc CDB
Do đó: ΔBDE đồng dạng với ΔCDB
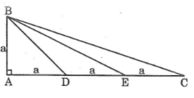

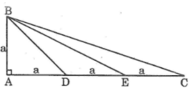

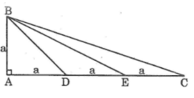


a) Ta có: AD=DE=EC(gt)
mà AD+DE+EC=AC
nên \(AD=DE=EC=\frac{AC}{3}=\frac{6}{3}=2cm\)
Áp dụng định lí pytago vào ΔADB vuông tại A, ta được:
\(DB^2=AD^2+AB^2\)
\(\Leftrightarrow DB^2=2^2+2^2=8\)
hay \(DB=\sqrt{8}=2\sqrt{2}cm\)
\(\Rightarrow\frac{DE}{DB}=\frac{2}{2\sqrt{2}}=\frac{1}{\sqrt{2}}\)(1)
Ta có: DC=DE+EC(E nằm giữa D và C)
hay DC=2+2=4cm
\(\Rightarrow\frac{DB}{DC}=\frac{2\sqrt{2}}{4}=\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}\)(2)
Từ (1) và (2) suy ra \(\frac{DE}{DB}=\frac{DB}{DC}\)(đpcm)
b) Xét ΔBDE và ΔCDB có
\(\frac{DE}{DB}=\frac{DB}{DC}\)(cmt)
\(\widehat{EDB}\) chung
Do đó: ΔBDE∼ΔCDB(c-g-c)