Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bạn tự vẽ nha
vì HB=HC=x nên AH là đường trung tuyến của tam giác ABC
nên BH=HC=\(\dfrac{1}{2}\)AH=\(\dfrac{1}{2}\)5=2,5
Ta có AB=AC=y nên BC.AH=AB.AC (htl)
\(\Leftrightarrow\)(BH+HC).AH=AB.AC\(\Leftrightarrow\)(2,5+2,5).5=y.y\(\Leftrightarrow\)25=2y
\(\Rightarrow\)y=\(\dfrac{25}{2}=12,5 \)

2/ Ta có
\(x^2+y^2\ge\frac{\left(x+y\right)^2}{2}=8\)
\(xy\le\frac{\left(x+y\right)^2}{4}\Leftrightarrow\frac{1}{xy}\ge\frac{4}{\left(x+y\right)^2}=\frac{1}{4}\)
Từ đó ta có
\(P\ge8+\frac{33}{4}=\frac{65}{4}\)
Đạt được khi x = y = 2

a) \(\sqrt{13^2-12^2}=\sqrt{\left(13-12\right)\left(13+12\right)}\)
\(=\sqrt{1.25}=5\)
b)\(\sqrt{4}\sqrt{36}-\sqrt{25}=\sqrt{2^2}\sqrt{6^2}-\sqrt{5^2}\)
\(=2.6-5=7\)
\(\sqrt{2x-1}\) xác định \(\Leftrightarrow2x-1\ge0\Leftrightarrow2x\ge1\)
\(\Leftrightarrow x\ge\dfrac{1}{2}\)
vậy với \(x\ge\dfrac{1}{2}\) thì \(\sqrt{2x-1}\) xác định
Bài 3:
a: BC=10cm
Xét ΔABC vuông tại A có sin C=AB/BC=3/5
nên góc C=37 độ
=>góc B=53 độ
b: AB*cosB+AC*cosC
=AB*AB/BC+AC*AC/BC
=AB^2/BC+AC^2/BC
=BC^2/BC
=BC

Áp dụng hẹ thức lượng trong tam giác vuông:
\(AB.AC=AH.BC=78\)
\(\Rightarrow AB=\dfrac{78}{AC}\)
Lại có:\(AB^2+AC^2=BC^2\Leftrightarrow\left(\dfrac{78}{AC}\right)^2+AC^2=169\)
\(\Leftrightarrow AC^4-169AC^2+6084=0\)\(\Leftrightarrow\left[{}\begin{matrix}AC=\sqrt{117}=3\sqrt{13}\\AC=\sqrt{52}=2\sqrt{13}\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}AB=2\sqrt{13}\\AB=3\sqrt{13}\end{matrix}\right.\)
Vậy \(AB=2\sqrt{13};AC=3\sqrt{13}\) hoặc \(AC=2\sqrt{13};AB=3\sqrt{13}\)
Xét \(\Delta\)ABC vuông tại A, đường cao AH
\(AB.AC=AH.BC=6.13=78\)
\(\rightarrow AC=\dfrac{78}{AB}\)
Xét \(\Delta ABC\) vuông tại A
\(\rightarrow AB^2+AC^2=BC^2\left(Pytago\right)\)
\(\rightarrow AB^2+\left(\dfrac{78}{AB}\right)^2=13^2\)
\(\rightarrow AB^2+\dfrac{6084}{AB^2}=169\)
\(\rightarrow AB^4+6084=169AB^2\)
\(\rightarrow AB^4-169AB^2+6084=0\)
Đặt \(t=AB^2>0\). Phương trình trở thành:
\(t^2-169t+6084=0\)
\(\Leftrightarrow t^2-117t-52t+6084=0\)
\(\Leftrightarrow t\left(t-117\right)-52\left(t-117\right)=0\)
\(\Leftrightarrow\left(t-52\right)\left(t-117\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t-52=0\\t-117=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=52\\t=117\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}AB^2=52\\AB^2=117\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}AB=\sqrt{52}=2\sqrt{13}\rightarrow AC=\dfrac{78}{2\sqrt{13}}=3\sqrt{13}\\AB=\sqrt{117}=3\sqrt{13}\rightarrow AC=\dfrac{78}{3\sqrt{13}}=2\sqrt{13}\end{matrix}\right.\)
Vậy hai cạnh góc vuông của tam giác vuông là \(3\sqrt{13}\) và \(2\sqrt{13}\)
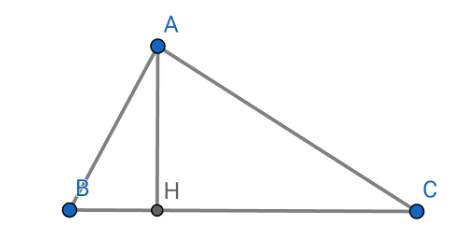

Với bài toán này, ta sử dụng hệ thức lượng trong tam giác.
a. Kiểm tra thấy \(AB^2+AC^2=BC^2\) nên tam giác ABC vuông tại A.
\(AH=\frac{AB.AC}{BC}=\frac{60}{13}\)
b. Áp dụng hệ thức lượng, ta thấy \(AB.EA=AH^2=AF.AC\)
c. Từ kết quả câu b và góc A vuông ta suy ra được \(\Delta AEF\sim\Delta ACB\left(c-g-c\right)\).

- Ap dung dinh ly pitago dao vao tam giac ABC ta co AB2+AC2=52+122=169=132 . ma BC2=132
- =>AB2+AC2=BC2=>Tam giac ABC vuong tai A
- Ke duong cao AH .Ap dung ti so luong giac vao tam giac vuong ABC ta co \(\frac{1}{AH^2}\)= \(\frac{1}{AB^2}\)+ \(\frac{1}{AC^2}\)=>\(\frac{1}{AH^2}\)= \(\frac{1}{5^2}\)+ \(\frac{1}{12^2}\)=>AH=\(\frac{60}{13}\)
3.Tu HE vuong goc voi AB , HF vuong goc voi AC =>HEA =900 , HFA =900 va BAC =900=>tu giac EHFA la hinh chu nhat =>goc AEF=EAH ma EAH=ACH vi cung phu voi goc HAC =>Ta chung minh duoc EAF ~ ABC 2.=>\(\frac{AB}{AF}\)= \(\frac{AC}{AE}\)=>AB\(\times\)AE = AF\(\times\)AC


Câu 1:
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{9^2}+\dfrac{1}{12^2}=\dfrac{1}{81}+\dfrac{1}{144}=\dfrac{25}{1296}\)
\(\Leftrightarrow AH^2=\dfrac{1296}{25}\)
hay \(AH=\dfrac{14}{5}=4.8cm\)
Vậy: AH=4,8cm
Câu 2:
Ta có: BC=BH+CH(H nằm giữa B và C)
hay BC=5+6=11(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow AB^2=5\cdot11=55\)
hay \(AB=\sqrt{55}cm\)
Vậy: \(AB=\sqrt{55}cm\)
Câu 4:
Không có hàm số nào không phải là hàm số bậc nhất
Theo định lý Py-ta-go ta có B C 2 = A B 2 + A C 2 ⇔ B C 2 = 169 ⇔ B C = 13
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
BC.AH = AB.AC <=> AH = A B . A C B C = 5.12 13 = 60 13
Vậy x = 60 13 ; y = 13
Đáp án cần chọn là: D