SN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 7 2023
AB/AC=3/4
=>BH/CH=9/16
=>BH/9=CH/16=(BH+CH)/(9+16)=15/25=0,6
=>BH=5,4cm; CH=9,6cm
24 tháng 5 2023
a: CH=16^2/25=10,24cm
BC=25+10,24=35,24cm
AB=căn 16^2+25^2=căn 881(cm)
b: AH=căn 12^2-6^2=6căn 3cm
CH=AH^2/HB=108/6=18cm
BC=6+18=24cm
c: BC=căn 5^2+25^2=5 căn 26cm
BH=5^2/5căn 26=5/căn 26(cm)
CH=5căn 26-5/căn 26=24,51(cm)
d: AB=căn 16^2-14^2=2căn15(cm)
e: AB=căn 2*8=4cm
AC=căn 6*8=4căn 3(cm)
T
1
H9
HT.Phong (9A5)
CTVHS
26 tháng 6 2023
Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow AC=\dfrac{AB\cdot3}{4}=6,75\left(cm\right)\)
\(\Delta ABC\) vuông tại A, áp dụng định lý Py-ta-go ta có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{9^2+6,75^2}=11,25\left(cm\right)\)
Theo hệ thức lượng giác vào tam giác vuông ABC đường cao AH có:
\(AB\cdot AC=BC\cdot AH\Rightarrow60,75=11,25AH\Rightarrow AH=\dfrac{60,75}{11,25}=5,4\left(cm\right)\)
\(\Rightarrow HB=\dfrac{AB^2}{BC}=\dfrac{9^2}{11,25}=7,2\left(cm\right)\)
O
2
AH
Akai Haruma
Giáo viên
20 tháng 9 2021
Lời giải:
Vì $AB:AC=3:4$ nên đặt $AB=3a; AC=4a$ với $a>0$
Áp dụng định lý Pitago:
$AB^2+AC^2=BC^2$
$\Leftrightarrow (3a)^2+(4a)^2=225$
$\Leftrightarrow 25a^2=225$
$\Rightarrow a=3$ (do $a>0$)
Áp dụng hệ thức lượng trong tam giác vuông:
$AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{9a^2}{15}=\frac{9.3^2}{15}=5,4$ (cm)
$AC^2=CH.CB\Rightarrow CH=\frac{AC^2}{BC}=\frac{16a^2}{15}=\frac{16.3^2}{15}=9,6$ (cm)
2 tháng 12 2021
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
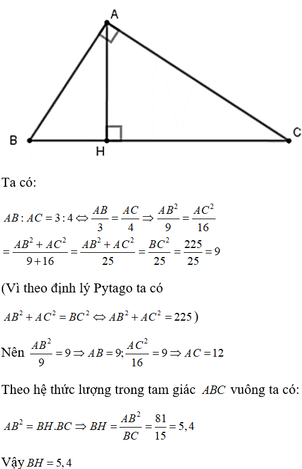
Ta có:\(\tan C\)=\(\frac{AB}{AC}\)=\(\frac{3}{4}\)\(\Rightarrow\)Góc C=\(\tan^{-1}\)(\(\frac{3}{4}\))\(\approx\)37 độ
lại có : AB=sinC.BC=sin37.15\(\approx\)9,027