Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta HAB\) vuông tại H \(\left(AH\perp BC\right)\),ta có:
\(AB^2=AH^2+BH^2\left(ĐLPytago\right)\\ \Rightarrow BH^2=AB^2-AH^2\\ \Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{7^2-2^2}=3\sqrt{5}\left(cm\right)\)
Xét \(\Delta ABC\) vuông tại A và có AH là đường cao \(\left(AH\perp BC\right)\),ta có:
\(AH^2=BH.CH\left(HTL\right)\\ \Rightarrow CH=\dfrac{AH^2}{BH}=\dfrac{2^2}{3\sqrt{5}}=\dfrac{4\sqrt{5}}{15}\left(cm\right)\)

hình tự vẽ nhé:
Áp dụng hệ thức lượng ta có:
\(AC^2=HC.BC=9BC\)
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\)\(400+9BC=BC^2\)
\(\Leftrightarrow\)\(BC^2-9BC-400=0\)
\(\Leftrightarrow\)\(\left(BC-25\right)\left(BC+16\right)=0\)
\(\Leftrightarrow\)\(BC=25\)
\(\Rightarrow\)\(AC^2=9.25=225\)
\(\Rightarrow\)\(AC=\sqrt{225}=15\)
Áp dụng hệ thức lượng ta có:
\(AB.AC=AH.BC\)
\(\Rightarrow\)\(AH=\frac{AB.AC}{BC}\)
\(\Rightarrow\)\(AH=\frac{20.15}{25}=12\)

ΔABC vuông cân tại A⇒AB=AC=4
Áp dụng hệ thức lượng ta có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{4^2}+\dfrac{1}{4^2}\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{16}+\dfrac{1}{16}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{8}\\ \Rightarrow AH^2=8\\ \Rightarrow AH=\sqrt{8}\)
Vì ΔABC vuông cân tại A
⇒ AB = AC = 4 cm
Áp dụng dịnh lí Py-ta-go vào ΔABC vuông tại A ta có:
BC2=AB2+AC2=42+42=32
⇔BC=\(4\sqrt{2}\)
Ta có:AB.AC=AH.BC (hệ thức lượng)
⇔\(AH=\dfrac{AB.AC}{BC}=\dfrac{4.4}{4\sqrt{2}}=2\sqrt{2}\left(cm\right)\)
Cho tam giác ABC vuông tại A, AH vuông góc với BC,có AH=2, tan B=1/3. Tính AB, AC. Mong mn giúp mình

Trong tam giác vuông ABH ta có:
\(tanB=\dfrac{AH}{BH}\Rightarrow BH=\dfrac{AH}{tanB}=6\)
Áp dụng định lý Pitago:
\(AB^2=AH^2+BH^2=40\)
\(\Rightarrow AB=2\sqrt{10}\)
Trong tam giác vuông ABC:
\(tanB=\dfrac{AC}{AB}\Rightarrow AC=AB.tanB=\dfrac{2\sqrt{10}}{3}\)

Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=5\)
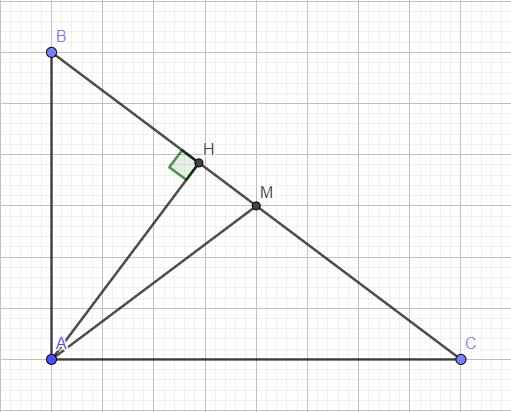
Trong tam giác vuông ABC, AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{5}{2}\)
Áp dụng hệ thức lượng:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12}{5}\)
Áp dụng định lý Pitago cho tam giác vuông AHM:
\(HM=\sqrt{AM^2-AH^2}=\dfrac{7}{10}\)

b: \(AN\cdot AC=AH^2\)
\(AC^2-HC^2=AH^2\)
Do đó: \(AN\cdot AC=AC^2-HC^2\)
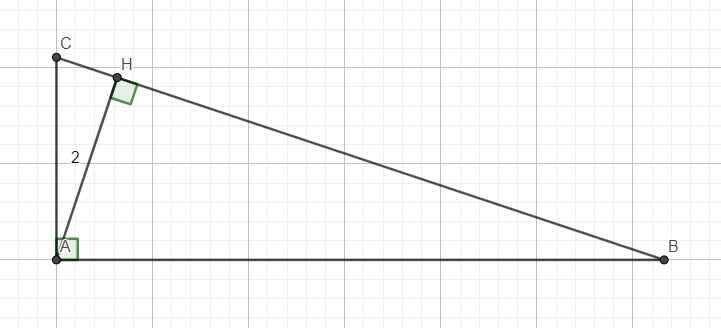
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow HB^2=4^2-2^2=12\)
\(\Leftrightarrow HB=2\sqrt{3}\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC=\dfrac{2^2}{2\sqrt{3}}=\dfrac{2\sqrt{3}}{3}\)
cảm ơn