Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔABE=ΔHBE
b: Xét ΔABC vuông tại A có
\(\sin C=\dfrac{AB}{BC}\)
=>AB=1/2BC
=>BH=1/2BC
=>H là trung điểm của BC
Xét ΔCBE có
H là trung điểm của BC
HK//BE
Do đó: K là trung điểm của CE
Ta có: ΔHCE vuông tại H
mà HK là đường trung tuyến
nên HK=KE=CE/2
=>ΔHKE cân tại K
mà \(\widehat{KEH}=60^0\)
nên ΔHKE đều

Bạn tự vẽ hình nha.
a,Xét tg ABE và tg HBE:
^BAE=^BHE=90*
^ABE=^HBE(BE là pg)
BE chung
=>tg ABE= tg HBE(ch-gn)
b,+,tg ABC có:^BAC=90*,^ABC=60*
=>^C=30*
+,tg BHE có: ^BHE=90*,^EBH=30*(^EHB=1/2ABC)
=>^HEB=60*
Mà HK // BE
=>^HBE=^EHK=60*(slt)
+, tg CHE có:^EHC=90*,^C=30*
=>HEC=60*
+,tg HEK có:
^EHK=60*,^HEC(^HEK)=60*
=>TG HEK đều(dhnb)
Phần c mik chỉ ghi các bước thôi còn bạn tự chình bày nhé.
c, +,CM:tg AEM=tg HEC(cgv-gnk)
=>AM=HC
+,CM:BM=BC
+,CM:tg BMI=tgBCI(cgc)
=>NM=NC
Xong r nha. Chúc bạn học tốt.

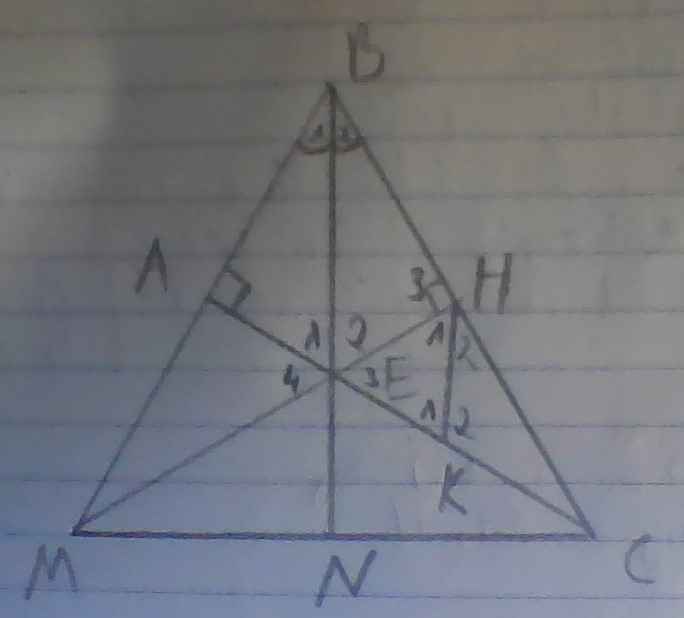
a) có BE là tia p/g của góc ABC
=> góc B1 = góc B2 = góc ABC/2 = 600 /2 = 300
có △ABC vuông tại A => △ABE vuông tại A
EH⊥BC=> △HBE vuông tại H
Xét △ vuông ABE và △vuông HBE có
góc B1 = góc B2
BE chung
=>△ vuông ABE =△vuông HBE ( cạnh huyền - góc nhọn)
b) có △ABE vuông tại A=> góc B1 + góc E1 = 900
góc E1 = 600 ( vì góc B1 = 300)
có △ vuông ABE =△vuông HBE
=> góc E1 = góc E2
mà HK//BE => góc E1 = góc K1 (ĐV)
và góc E2 = góc H1 (SLT)
=> góc E1 = góc E2 = góc K1=góc H1 = 600
=> △HEK đều
c) có góc E1 = góc E2 ; góc E3 = góc E4
=>góc E1 +góc E4 = góc E2 + góc E3
=> góc BEM= góc BEC
Xét △BEM và △ BEC có
góc B1 = góc B2
BE chung
góc BEM= góc BEC
=> △BEM = △ BEC (g.c.g)
=>BM=BC
=>△BMC cân tại B
trong △BMC có BN là đường p/g xuất phát từ đỉnh B
lại có △BMC cân tại B
=> BN cũng là đường trung tuyến xuất phát từ đỉnh B
=> N là trung điểm của MC
=> NM=NC

Bài 5:
a) Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABE=ΔHBE(cạnh huyền-góc nhọn)

góc ABE=góc HBE=60/2=30 độ
=>góc AEB=góc HEB=60 độ
=>góc AEH=120 độ
HK//BE
=>góc KHE=góc HEB=60 độ
góc KEH=180-120=60 độ
Xét ΔKEH có góc KHE=góc KEH=60 độ
nên ΔKEH đều

a) xét \(\Delta\)vuông ABE và\(\Delta\)vuông HBE có:
BE là cạnh chung
gcABE=gcHBE(BE là tia p.g của gc ABC)
=> tg ABE=tgHBE(cạnh huyền góc nhọn)
b) theo câu a: tg ABE= tg HBE (cmt)=>AB=BH (1)
trong tg vuông ABC có: gc B =60o=> gc C=30o
=> AB=\(\frac{1}{2}\) BC(2)
=> BH = \(\frac{BC}{2}\)mà H thuộc BC => H là trung điểm BC
xét tg BCE có:H là TĐ của BC(cmt)
HK//BE(gt)=> K là trung điểm EC
xét tg vuông HEC có: HK là đường trung tuyến ứng vs cạnh huyền
=> HK=EK= \(\frac{EC}{2}\)=> tg HEK cân ở K
lại có:gc EKH = gc ACB+gc KHC( góc ngoài cuả tgHKC)
gc KHC=gc EBC=30o( đồng vị ,HK//BE)
do đó gc EHK=gc ACB+gc EBC=30+30=60o
tam giác cân có 1 góc = 60 o là tam giác đều
c)(nhiều cách lúm)
trong tg vuông HBM: gc HBM= 60o=>gc HMB= 30o
=>\(BH=\frac{1}{2}BM\)mà BH= \(\frac{1}{2}BC\)(cmt )
=> BM=BC=> tg BMC cân ở B
BN là đường p.g của gcMBC
=> BN đồng thời là đường trung trực của tgMBC hay của cạnh MC
Có nhiều cách lắm nhưng mình làm cách này luôn
hình như cái này rõ hơn