Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

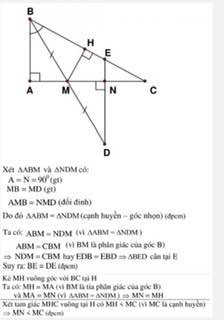
a) Xét tam giác \(ABM\) và tam giác \(NDM\):
\(\widehat{BAM}=\widehat{DNM}\left(=90^o\right)\)
\(MB=MD\)
\(\widehat{AMB}=\widehat{NMD}\)
Suy ra \(\Delta ABM=\Delta NDM\) (cạnh huyền - góc nhọn)
b) \(\Delta ABM=\Delta NDM\) suy ra \(\widehat{ABM}=\widehat{NDM}\)
mà \(\widehat{ABM}=\widehat{EBM}\).
suy ra \(\widehat{NDM}=\widehat{EBM}\) suy ra tam giác \(EBD\) cân tại \(E\)
suy ra \(BE=DE\).

Xét ΔABM và ΔNDM có:
góc A=góc N (=90 độ)
MB=MD (gt)
góc AMB=góc NMD (2 góc đối đỉnh)
⇛ΔABM=ΔNDM(g-c-g)

Xét \(\Delta ABM\)và \(\Delta NDM\)có: \(\hept{\begin{cases}\widehat{A}=\widehat{DNM}=90^o\left(gt\right)\\MB=MD\left(gt\right)\\\widehat{AMB}=\widehat{NMD}\end{cases}}\Rightarrow\Delta ABM=\Delta NDM\left(ch-gn\right)\left(đpcm\right)\)
Ta có \(\widehat{ABM}=\widehat{NDM}\left(\Delta ABM=\Delta NDM\right)\)
\(\widehat{ABM}=\widehat{CBM}\)(BM là phân giác \(\widehat{B}\))
\(\Rightarrow\widehat{NDM}=\widehat{CBM}\)hay \(\widehat{EDB}=\widehat{EBD}\)
\(\Rightarrow\Delta BED\)cân tại E
=> BE=DE (đpcm)
Kẻ MH vuông góc với BC tại H
Ta có MH=MA (vì BM là tia phân giác của \(\widehat{B}\))
và MA=MN (\(\Delta ABM=\Delta NDM\))
=> MN=MH
Xét \(\Delta MHC\)vuông tại H có MH<MC (vì MC là cạnh huyền)
=> MN<MC (đpcm)

tham khảo
kẻ thêm MK⊥BC⊥BC
ta có ΔABM=ΔKBM(ch.cgn)ΔABM=ΔKBM(ch.cgn)
lí do vì góc B1=góc B2(do BM phân giác),
góc BKM=góc BAM=90oo, cạnh BM chung
từ đó=>AM=MK(các cạnh t ứng)(1)
chứng minh ΔMND=ΔMAB(ch.cgn)ΔMND=ΔMAB(ch.cgn)
do góc M1=M2(đối đỉnh), MB=MD(gt), góc DNM=góc BAM(=90 độ)
=>AM=MN(2) từ(1)(2)=>MN=MK
trong tam giác MKC vuông tại K thì cạnh huyền MC lớn nhất
=>MC>MK<=>MC>MN(dpcm)

Xét △AMD và △CMB
Có: AM = MC (M là trung điểm)
AMD = CMB (2 góc đối đỉnh)
MD = MB (gt)
=> △AMD = △CMB (c.g.c)
=> AD = BC (2 cạnh tương ứng)
b, Xét △ABM và △CDM
Có: AM = MC (gt)
BMA = CMD (2 góc đối đỉnh)
MB = MD (gt)
=> △ABM = △CDM (c.g.c)
=> BAM = DCM (2 góc tương ứng)
Mà BAM = 90o
=> DCM = 90o
=> AC ⊥ CD
c, Vì BN // AC (gt)
=> BNC = ACD (2 góc đồng vị)
Mà ACD = 90o (câu b)
=> BNC = 90o
Xét tam giác BND vuông tại N có:
NM là đường trung tuyến ứng với cạnh huyền BD => NM = 1/2 . BD = BM
Xét △ABM vuông tại A và △CNM vuông tại C
Có: AM = MC (gt)
BM = MN (cmt)
=> △ABM = △CNM (ch-cgv)

a: Xét ΔABM vuông tại A và ΔNDM vuông tại N có
MB=MD
góc AMB=góc NMD
=>ΔABM=ΔNDM
b: góc EDB=góc ABM
=>góc EBD=góc EDB
=>ΔEBD cân tại E
Vẽ hộ mình cái hình với
vẽ hộ mình cái hình với