Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xet ΔABC vuông tại A và ΔHBA vuôngtại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*BC
b: Xét ΔAEB và ΔIEC có
góc BAE=góc EIC
góc AEB=góc IEC
=>góc ABE=góc ICE=góc IBC
=>ΔIEC đồng dạng với ΔICB
=>IE/IC=IC/IB
=>IC^2=IE*IB
c: Xét ΔBNC có
BI vừa là phân giác, vừa là đường cao
=>ΔBNC cân tại B
=>I là trung điểm của NC
ΔNAC vuông tại A
mà I là trung điểm của NC
nên IA=IN=IC
=>IN^2=IE*IB
và IA=IM
nên IM^2=IE*IB
=>IM/IE=IB/IM
=>ΔIMB đồng dạng với ΔIEM
=>góc IMB=90 độ
=>ĐPCM

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc HBA chung
Do đó:ΔHBA\(\sim\)ΔABC
b: ta có: ΔHBA\(\sim\)ΔABC
nên BH/BA=BA/BC
hay \(BA^2=BH\cdot BC\)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng vơi ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*BC
b: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2
=>AE*AB=AF*AC

1: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc ACB chung
Do đó: ΔABC\(\sim\)ΔHAC
2: \(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
Xét ΔABC có AM là phân giác
nên BM/AB=CM/AC
=>BM/3=CM/4
Áp dụng tính chất của dãy tr số bằng nhau, ta được:
\(\dfrac{BM}{3}=\dfrac{CM}{4}=\dfrac{BM+CM}{3+4}=\dfrac{25}{7}\)
Do đó: BM=75/7(cm); CM=100/7(cm)

câu B: Gọi I, K lần lượt là trung điểm của HC, HB. Chứng minh 1/OH^2=1/Ok^2+1/OI^2
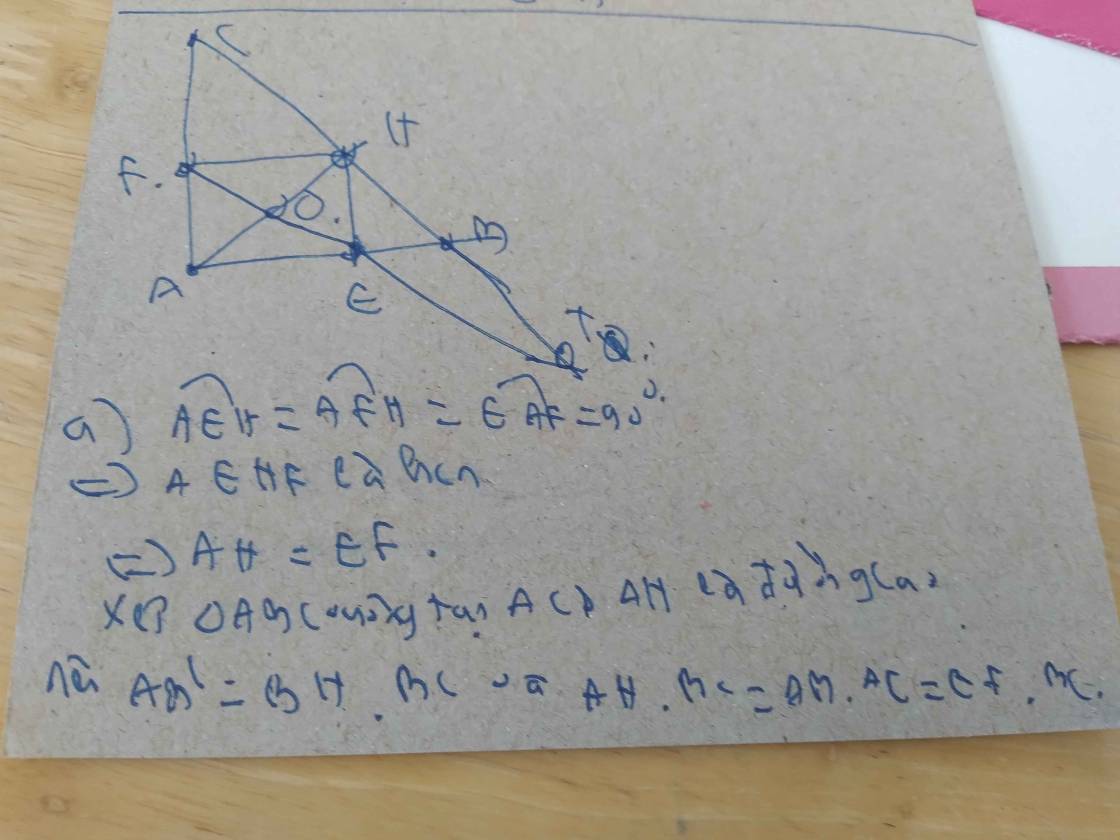

***Hình bạn tự vẽ nha***
a, Xét tam giác ABC và tam giác BHA có :
Góc ABC chung
Góc BAC = góc BHA ( =90°)
==> Tam giác ABC đồng dạng tam giác HBA ( g.g )
==> AB/HB = BC/AB ==> AB^2 = HB. BC