Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
\(\widehat{ABM}=\widehat{DBM}\)
Do đó: ΔBAM=ΔBDM
=>BA=BD và MA=MD
b: Xét ΔBDE vuông tại D và ΔBAC vuông tại A có
BD=BA
\(\widehat{DBE}\) chung
Do đó: ΔBDE=ΔBAC
c: Xét ΔMKA vuông tại K và ΔMHD vuông tại H có
MA=MD
\(\widehat{KMA}=\widehat{HMD}\)
Do đó: ΔMKA=ΔMHD
=>MK=MH và AK=HD
Xét ΔNKM vuông tại K và ΔNHM vuông tại H có
NM chung
MK=MH
Do đó: ΔNKM=ΔNHM
=>NK=NH và \(\widehat{KMN}=\widehat{HMN}\)
=>MN là phân giác của góc HMK
d: NK+KA=NA
NH+HD=ND
mà NK=NH và KA=HD
nên NA=ND
=>N nằm trên đường trung trực của AD(1)
MA=MD
=>M nằm trên đường trung trực của AD(2)
BA=BD
=>B nằm trên đường trung trực của AD(3)
Từ (1),(2),(3) suy ra B,M,N thẳng hàng

Hình tự vẽ
a, \(\Delta BAM\)và \(\Delta BDM\)có
\(\widehat{ABM}=\widehat{DBM}\left(gt\right)\)
\(AM\): cạnh chung
\(\widehat{BAM}=\widehat{BDM}\left(=90^o\right)\)
\(\Rightarrow\Delta BAM=\Delta BDM\left(ch-gn\right)\)
\(\Rightarrow BA=BD\)(2 cạnh tương ứng )
Để nghĩ tiếp :(
Ta có:
∠AMB+∠ABM=90o
∠BMD+∠MBD=900
Mà ∠AMB=∠BMD (gt)
=> ∠ABM=∠MBD
Xét ΔBAM và ΔBAM có:
∠ABM=∠MBD (gt)
BM chung
∠ABM=∠MBD (cmt)
=> ΔBAM = ΔBAM (g-c-g)
=> BA=BD (2 cạnh tương ứng)
b,Xét ΔABC và ΔDBE có:
∠ABC chung
∠BAC=∠BDM=90o
BA=BD (cmt)
=> ΔABC = ΔDBE (g-c-g)
c,Ta có
BC⊥ED
AK⊥ED
=> BC//AK hay BC//AN
=> ∠ANM=∠MBC ( 2 góc slt) (1)
Mà:
DH⊥AC
BA⊥AC
=> BA//DH hay BA//DN
=> ∠MND=∠ABM ( 2 góc so le trong) (2)
Mà ∠ABM=∠MBD ( vì BM là tia phân giác của góc ABC)
Từ(1) và (2) =>∠ANM=∠MND
=> NM là tia phân giác của góc HMK
d,Ta có BM là tia phân giác của góc ABC (3)
Và NM là tia phân giác của góc HMK
Vì ∠ANM=∠MBC
∠MND=∠ABM
=> ∠ANM=∠MBC=∠MND=∠ABM
=> BN là tia phân giác của góc ABC (4)
Từ (3) và (4) => B,M,N thẳng hàng

a/ Xét tam giác ABM và tam giác EBM:
+ ^A = ^AEB ( = 90o)
+ BM chung
+ ^ABM = ^EBM ( do BM là phân giác ^B)
=> Tam giác ABM = Tam giác EBM (ch - gn)
b/ Ta có: ^A = ^B + ^C = 90o (do tam giác ABC vuông tại A)
Mà ^C = 30o (gt)
=> ^B = 60o
Tam giác ABM = Tam giác EBM (cmt)
=> AB = EB (cặp cạnh tương ứng)
=> Tam giác ABE cân tại B
Lại có: ^B = 60o (cmt)
=> Tam giác ABE đều

a) Xét ΔABM vuông tại A và ΔHBM vuông tại H có
BM chung
\(\widehat{ABM}=\widehat{HBM}\)(BM là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABM=ΔHBM(cạnh huyền-góc nhọn)

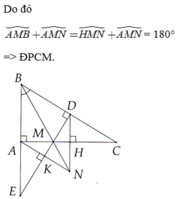


a) 2 tam giác = nhau (cạnh huyền góc nhọn )
b) gọi i guiao điểm BM và AE .2 tam giác trên bằng nhau => AB=BE Nên tam giác ABE cân tại B dễ dàng cm 2 tam giác ABi và BIE =nhau theo trường hoợ (g-c-g).tự cm rta đc vuông góc
c) Xét 2 tam giác MEC và AMN . góc MAB =90 độ,góc MEC= 90 độ. AM=ME ( vì tam giacs ABM= tam giác BEM). gocs AMN= gocs EMC.xong 2 tam giác bằng nhau theo trường hợp (g-c-g)