Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho Δ ABC vuông tại A, AB = 9cm, AC = 12cm, đường cao AH, phân giác BD. Vẽ DC ⊥ BC, đường thẳng DE cắt đường thẳng AB tại F
a) Tính BH, CH
Ap dung dl Pytago vao trong tam giac vuong ABC ta co:
BC^2 = AB^2 + AC^2
=> BC = 15
AH la duong cao trong tam giac vuong ABC
=> 1/AH^2 = 1/AB^2 + 1/AC^2
=> AH = 7,2
Ap dung dl PYtago vao trong tam giac vuong AHB ta duoc:
BH^2 = AB^2 - AH^2
=> BH = 5,4
BC = BH + HC
=> HC = 9,6
b) Chứng minh Δ EBF đồng dạng Δ EDC
Tam giac EDC dong dang tam giac ADF(g,g,g)
=> Goc AFD = goc ECD
Ma AFD = 90 - goc B
=> Goc EDC = Goc B
Xet tam giac vuong EBF va tam giac vuong EDC ta co:
+) Goc A1 = goc E = 90
+) Goc B = Goc EDC
+) Goc BFE = Goc C
=> Δ EBF đồng dạng Δ EDC

) Chứng minh Δ EBF đồng dạng Δ EDC Tam giac EDC dong dang tam giac ADF(g,g,g)=> Goc AFD = goc ECD Ma AFD = 90 - goc B => Goc EDC = Goc BXet tam giac vuong EBF va tam giac vuong EDC ta co:+) Goc A1 = goc E = 90+) Goc B = Goc EDC+) Goc BFE = Goc C=> Δ EBF đồng dạng Δ EDC

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
AH=9*12/15=7,2cm
b: ΔHAB vuông tại H có HM vuông góc AB
nên MH^2=MA*MB

$#Shả$
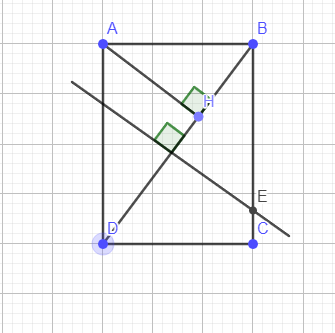
`a)` Xét `\triangleAHB` và `\triangleBCD` ta có `:`
`\hat{AHB}=\hat{BCD}=90^{o}`
`\hat{ABH}=\hat{BDC} ` (slt)
Vậy `\triangleAHB ` $\backsim$ `\triangleBCD` (g-g)
a) △AHB và △BCD có: \(\widehat{AHB}=\widehat{BCD}=90^0\); \(\widehat{ABH}=\widehat{BDC}\) (AB//DC).
\(\Rightarrow\)△AHB∼△BCD (g-g).
b) △ABD có: \(BD^2=AD^2+AB^2\Rightarrow BD=\sqrt{AD^2+AB^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
△AHB∼△BCD \(\Rightarrow\dfrac{AH}{BC}=\dfrac{AB}{BD}=\dfrac{HB}{CD}\)
\(\Rightarrow\left[{}\begin{matrix}AH=\dfrac{AB.BC}{BD}=\dfrac{3.4}{5}=2,4\left(cm\right)\\HB=\dfrac{AB.CD}{BD}=\dfrac{3.3}{5}=1,8\left(cm\right)\end{matrix}\right.\)
\(\Rightarrow S_{AHB}=\dfrac{1}{2}AH.HB=\dfrac{1}{2}.2,4.1,8=2,16\left(cm^2\right)\)
c) ABCD là hình chữ nhật, AC cắt BD tại O.
\(\Rightarrow\)O là trung điểm của AC và BD.
BD⊥DE tại D, CF⊥DE tại F. \(\Rightarrow\)BD//CF.
-△ODE có: IF//OD \(\Rightarrow\dfrac{IF}{OD}=\dfrac{EI}{EO}\).
-△OBE có: IC//OB \(\Rightarrow\dfrac{IC}{OB}=\dfrac{EI}{EO}=\dfrac{IF}{OD}\Rightarrow IC=IF\Rightarrow\)I là trung điểm CF.

(Tự vẽ hình)
a) Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2=9^2+12^2=225\Rightarrow BC=15\left(cm\right)\)
Xét \(\Delta AHB\) và \(\Delta CAB\) có:
\(\widehat{AHB}=\widehat{CAB}=90^0\);
\(\widehat{B}\) chung
\(\Rightarrow\Delta AHB\sim\Delta CAB\) (g.g)
b) Do \(\Delta AHB\sim\Delta CAB\Rightarrow\dfrac{AH}{AB}=\dfrac{AC}{BC}\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{9.12}{15}=7,2\left(cm\right)\)
c) Xét \(\Delta BAD\) và \(\Delta BHK\) có:
\(\widehat{BAD}=\widehat{BHK}=90^0\)
\(\widehat{ABD}=\widehat{HBK}\) (tính chất phân giác)
\(\Rightarrow\Delta BAD\sim\Delta BHK\left(g.g\right)\Rightarrow\dfrac{BA}{BD}=\dfrac{BH}{BK}\Rightarrow BA.BK=BH.BD\)
ai đó làm ơn giải hộ mình bài này với
a) Áp dụng định lý PYTAGO vào tam giác ABC có
BC^2=AB^2+AC^2
= 9^2+12^2=225
BC= 15
Sabc= 1/2.AB.AC = 54 mà Sabc = 1/2.AH.BC
=> 1/2.AH = Sabc: BC = 3.6=> AH =7,2