Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
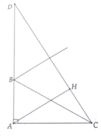
a,i, Tìm được AB=3cm và AC = 6 3 cm
ii, Ta có: A B B D = A C B C = cos A B C ^ = cos 60 0 = cos A C D ^ = A C C D
b, Ta có: 1 A H 2 = 1 A C 2 + 1 A D 2
a) Có AH2=HF.HD \(\rightarrow\)\(\frac{AH}{HF}=\frac{HD}{AH}\)
Xét \(\Delta\)AHD và \(\Delta\)FHA có:
\(\widehat{AHD}=\widehat{FHA}=90^o\)
\(\frac{AH}{HF}=\frac{HD}{AH}\)( chứng minh trên)
\(\rightarrow\Delta\)AHD\(\approx\)\(\Delta\)FHA (c-g-c)
\(\rightarrow\)\(\widehat{ADH}=\widehat{FAH}\)( 2 góc tương ứng)
mà \(\widehat{ADH}+\widehat{HAD}=90^o\)
nên \(\widehat{FAH}+\widehat{HAD}=90^o\)
hay \(\widehat{FAD}=90^o\)\(\rightarrow\Delta\)ADF vuông tại A
c: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABD vuông tại A có AI là đường cao ứng với cạnh huyền BD, ta được:
\(BI\cdot BD=AB^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BI\cdot BD=BH\cdot BC\)
a: Xét ΔABC vuông tại A có \(cosB=\dfrac{BA}{BC}\)
=>\(\dfrac{BA}{6}=cos60=\dfrac{1}{2}\)
=>BA=3(cm)
ΔACB vuông tại A
=>\(BA^2+AC^2=BC^2\)
=>\(AC^2+3^2=6^2\)
=>\(AC^2=27\)
=>\(AC=3\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(CH\cdot CB=CA^2\)
=>\(CH\cdot6=27\)
=>CH=4,5(cm)
b: Sửa đề: \(\dfrac{1}{KD\cdot KC}=\dfrac{1}{AD^2}+\dfrac{1}{AC^2}\)
Xét ΔACD vuông tại A có AK là đường cao
nên \(AK^2=KD\cdot KC\)
Xét ΔACD vuông tại A có AK là đường cao
nên \(\dfrac{1}{AK^2}=\dfrac{1}{AD^2}+\dfrac{1}{AC^2}\)
=>\(\dfrac{1}{KD\cdot KC}=\dfrac{1}{AD^2}+\dfrac{1}{AC^2}\)
c: \(\widehat{ABC}+\widehat{CBD}=180^0\)(hai góc kề bù)
=>\(\widehat{CBD}+60^0=180^0\)
=>\(\widehat{CBD}=120^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=90^0-60^0=30^0\)
Xét ΔDBC có BD=BC
nên ΔBDC cân tại B
=>\(\widehat{BDC}=\widehat{BCD}=\dfrac{180^0-\widehat{DBC}}{2}=30^0\)
Xét ΔACB vuông tại A và ΔADC vuông tại A có
\(\widehat{ACB}=\widehat{ADC}\)
Do đó:ΔACB đồng dạng với ΔADC
=>\(\dfrac{BC}{CD}=\dfrac{AC}{AD}\)
=>\(\dfrac{BC}{AC}=\dfrac{CD}{AD}\)
mà BC=BD
nên \(\dfrac{BD}{AC}=\dfrac{CD}{AD}\)
=>\(\dfrac{BD}{CD}=\dfrac{AC}{AD}=tanD\)
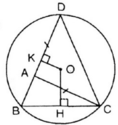
a) Xét ΔABC có: BC < AB + AC (Bất đẳng thức tam giác)
Mà AD = AC (gt)
⇒ BC < AB + AD = BD
Mà OH là khoảng cách từ O đến dây BC
OK là khoảng cách từ O đến dây BD
⇒ OH > OK.( định lý về khoảng cách từ tâm đến dây)
b) Vì BD > BC
⇒ 
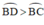
Kiến thức áp dụng
+ Trong một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn
+ Trong một đường tròn, dây lớn hơn căng cung lớn hơn.
a: Xét ΔBAC vuông tại A có
\(AC=6\cdot\sin60^0\)
hay \(AC=3\sqrt{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AB^2=9\)
hay AB=3cm
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9}{6}=1.5\left(cm\right)\\CH=\dfrac{27}{6}=4.5\left(cm\right)\end{matrix}\right.\)
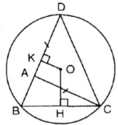
Xét ΔABC có: BC < AB + AC (Bất đẳng thức tam giác)
Mà AD = AC (gt)
⇒ BC < AB + AD = BD
Mà OH là khoảng cách từ O đến dây BC
OK là khoảng cách từ O đến dây BD
⇒ OH > OK.( định lý về khoảng cách từ tâm đến dây)
GIẢI: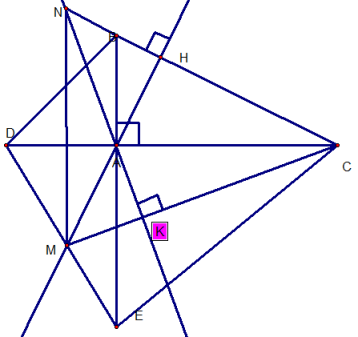
a) Xét Δ ABC và Δ AED, ta có :
AB = AD (gt)
AC = AD (gt)
=> Δ ABC = Δ AED (hai cạnh góc vuông)
=> BC = DE
Xét Δ ABD, ta có :
=> AD 
=>
=> Δ ABD vuông tại A.
mà : AB = AD (gt)
=> Δ ABD vuông cân tại A.
=>
cmtt :
=>
mà : 
=> BD // CE
b) Xét Δ MNC, ta có :
NK
MH
NK cắt MH tại A.
=> A là trực tâm. = > CA là đường cao thứ 3.
=> MN
mà : AB
=> MN // AB.
c) Xét Δ AMC, ta có :
=>
=> Δ AMC cân tại M
=> AM = ME (1)
Xét Δ AMI và Δ DMI, ta có :
IM cạnh chung.
mặt khác : 
mà :
=>
=> Δ AMI = Δ DMI (góc nhọn – cạnh góc vuông)
=> MA = MD (2)
từ (1) và (2), suy ta : MA = ME = MD
ta lại có : ME = MD = DE/2 (D, M, E thẳng hàng)
=>MA = DE/2.