Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)xét tg ABC và tg MDC có: BAC=DMC=90, ^C chung
=>tg ABC đ.dạng vs tg MDC(g.g)
b)xét tg ABC và tg MBI có: CAB=BMI=90, ^B chung
=>tg ABC đ.dạng vs tg MBI(g.g) =>AB/MB=BC/BI=>AB.BI=BM.BC(đpcm)
a) Xét \(\Delta ABC\)và \(\Delta MDC\)
Ta có: \(\widehat{BAC}=\widehat{DMC}=90^o\)
\(\widehat{C}\)là góc chung
\(\Rightarrow\Delta ABC~\Delta MDC\left(g-g\right)\)
b) Xét \(\Delta BIM\)và \(\Delta BCA\)
Ta có: \(\widehat{IMB}=\widehat{CAB}=90^o\)
\(\widehat{B}\) là góc chung
\(\Rightarrow\Delta BIM~\Delta BCA\left(g-g\right)\)
\(\Rightarrow\frac{BI}{BC}=\frac{BM}{BA}\)
\(\Rightarrow BI\text{.}BA=BM.BC\)
C H I B D A

A B C M H D
a, Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A , ta có :
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC^2=BC^2-AB^2\)
\(\Rightarrow AC^2=25^2-20^2\)
\(\Rightarrow AC^2=225\)
\(\Rightarrow AC=15cm\)
Vậy AC = 15cm .
b,Xét tam giác AMC và tam giác HMB có :
góc MAC = góc MHB = 90độ
góc AMC = góc HMB ( đối đỉnh )
Do đó : tam giác AMC đồng dạng với tam giác HMB ( g.g )
c,Xét tam giác ADB và tam giác AMC có :
góc BAD = góc CAM = 90độ
góc ABD = góc ACM ( vì tam giác AMC đồng dạng với tam giác HMB )
Do đó : tam giác ADB đồng dạng với tam giác AMC ( g.g )
\(\Rightarrow\frac{AC}{AB}=\frac{AM}{AD}\)
\(\Rightarrow AC.AD=AM.AB\)
d, Xét tam giác DBC có BA cắt HC tại M :
\(CH\perp BD\)
\(BA\perp DC\)
\(\Rightarrow\)M là trực tâm của tam giác DBC
Vậy DM vuông góc với BC .
Học tốt

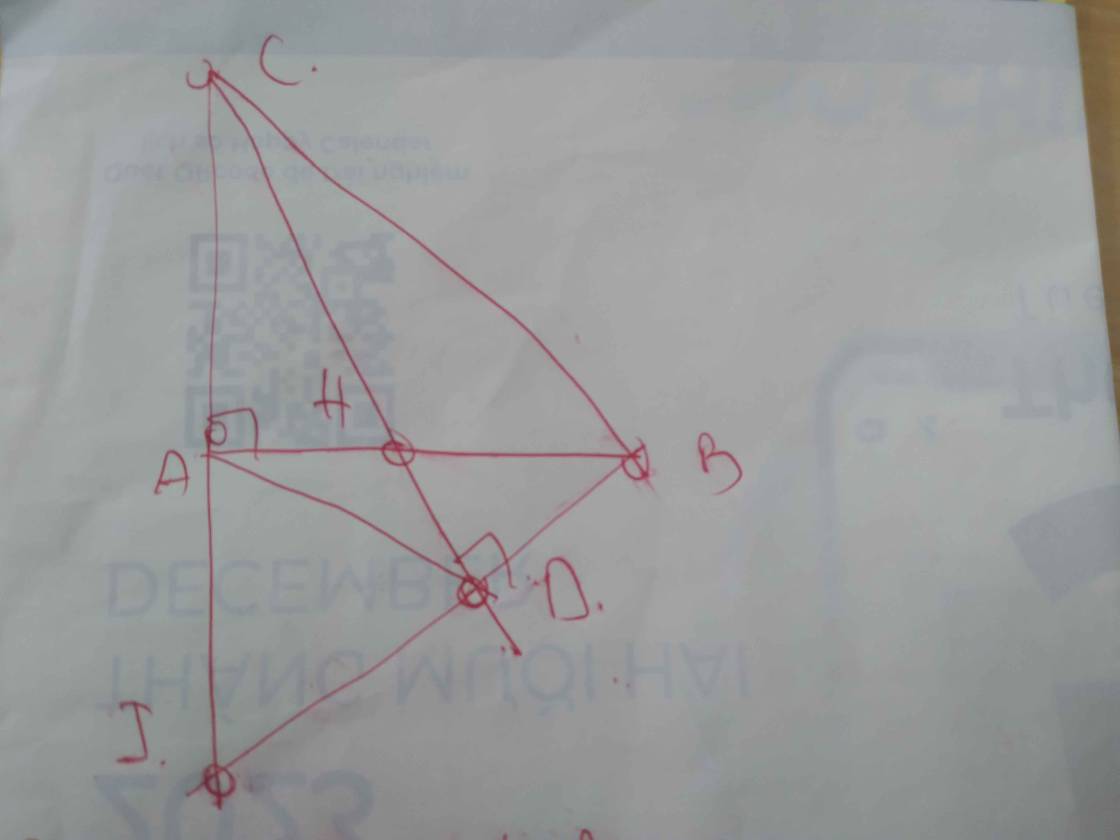

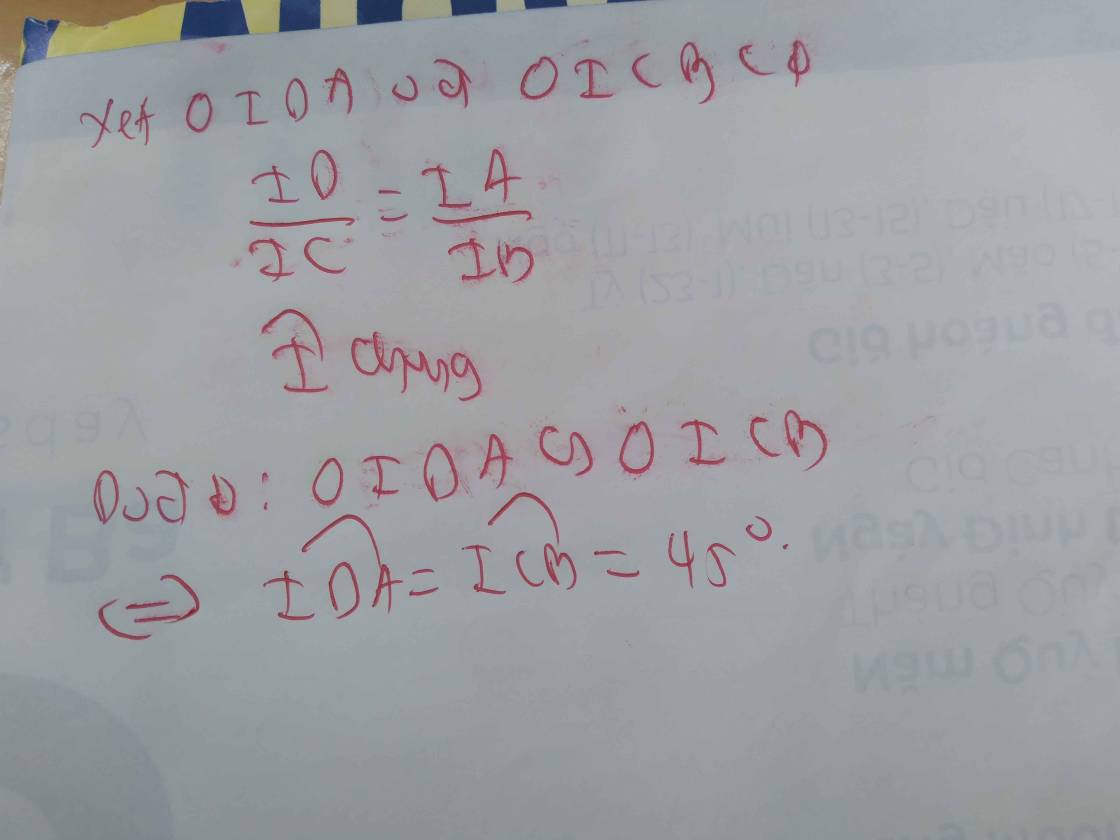

a: XétΔIDC vuông tại D và ΔIAB vuông tại A có
góc I chung
=>ΔIDC đồng dạng với ΔIAB
b: ΔIDC đồng dạng với ΔIAB
=>ID/IA=IC/IB
=>ID/IC=IA/IB
=>ΔIDA đồng dạng với ΔICB
=>góc IDA=góc ICB=45 độ